A MODIFIED TIKHONOV REGULARIZATION METHOD FOR THE CAUCHY PROBLEM OF LAPLACE EQUATION?
Fan YANG(楊帆)Chuli FU(傅初黎i)Xiaoxiao LI(李曉曉)
1.School of Science,Lanzhou University of Technology,Lanzhou 730050,China
2.School of Mathematics and Statistics,Lanzhou University,Lanzhou 730000,China
E-mail:yfggd114@163.com;fuchuli@lzu.edu.cn;lixiaoxiaogood@126.com
A MODIFIED TIKHONOV REGULARIZATION METHOD FOR THE CAUCHY PROBLEM OF LAPLACE EQUATION?
Fan YANG(楊帆)1,2?Chuli FU(傅初黎i)2Xiaoxiao LI(李曉曉)1
1.School of Science,Lanzhou University of Technology,Lanzhou 730050,China
2.School of Mathematics and Statistics,Lanzhou University,Lanzhou 730000,China
E-mail:yfggd114@163.com;fuchuli@lzu.edu.cn;lixiaoxiaogood@126.com
In this paper,we consider the Cauchy problem for the Laplace equation,which is severely ill-posed in the sense that the solution does not depend continuously on the data.A modifed Tikhonov regularization method is proposed to solve this problem.An error estimate for the a priori parameter choice between the exact solution and its regularized approximation is obtained.Moreover,an a posteriori parameter choice rule is proposed and a stable error estimate is also obtained.Numerical examples illustrate the validity and efectiveness of this method.
Cauchy problem for Laplace equation;ill-posed problem;a posteriori parameter choice;error estimate
2010 MR Subject Classifcation35R25;47A52;35R30
1 Introduction
The Cauchy problem for the Laplace equation has been extensively investigated in many practical areas.For example,some problems related to the geophysics[1,2],plasma physics[3], cardiology[4],bioelectric feld problems[5]and non-destructive testing[6].In the Hadamard’s famous paper[7],this problem is frstly introduced as a classical example of ill-posed problems, which shows that any small change of the data may cause dramatically large errors in the solution.Thus,it is impossible to solve this problem using classical numerical methods and requires special techniques,e.g.,regularization.There have been many papers devoted to this subject,such as the Fourier method[8],the central diference method[9],the quasi-reversibility method[10-13],the Tikhonov regularization method[14],the conjugate gradient method[15], the moment method[16-18],the wavelet method[19-20],the mollifcation method[21],the fundamental solutions[22],and etc.
In this paper,we consider the following Cauchy problem for the Laplace equation in a strip domain[23]:
the solution u(x,y)for 0<x<1 will be determined from the noisy data φδ(y)which satisfes
Problem(1.1)is severely ill-posed.However,to our knowledge,there are few papers devoted to the error estimates of regularization methods.In this paper,we will consider not just the a priori choice of the regularization parameter for the modifed Tikhononv regularization method, but also the a posteriori choice of the regularization parameter will be given for problem(1.1).
The modifed Tikhonov regularization was based on the Tikhonov regularization method. Skillfully modifed the penalty term of the Tikhonov functional,a better flter which flters the high frequencies of the measured data was obtained.This idea initially came from Carasso,who modifed the flter gained by the Tikhonov regularization method,and the order optimal error estimate was obtained in[24].By this method,Zhao[25]considered backward heat equation,Fu [26]considered the inverse heat conduction problem on a general sideways parabolic equation. Feng[27]used this method to consider the Cauchy problem for the Helmholtz equation.Cheng [28,29]used this method to consider the spherically symmetric inverse problem.Yang[30,31] used this method to consider the identifcation unknown source.
The plan of this paper is as follows.In Section 2 we simply analyze the ill-posedness of the Cauchy problem for Laplace equation and propose the modifed Tikhonov regularization method.In Section 3 we provide some stability and convergence estimates for the Cauchy problem.In Section 4,some numerical examples are proposed to show the efectiveness of this method.Section 5 puts an end to this paper with a brief conclusion.
2 Preliminaries
In this section,we give some auxiliary results which is needed in next section.For g(y)∈L2(R),?g(ξ)denotes its Fourier transform defned by
Let‖·‖denote the norm in L2(R).Then there holds the Parseval formula:
The application of the Fourier transform technique to problem(1.1)with respect to the variable y yields the following problem in frequency space:
It is easy to obtain that the solution of problem(2.3)is
whereμis the regularization parameter.It can be verifed that φμ,δ(x)is the solution of the following equation[32]:
From(2.5),we can see that T1:L2(R)→L2(R)is linear,compact and one-to one.From(2.5), we can also fnd
Due to Parseral formula,we have
From(2.8),we obtain
Note(2.11)and(2.12),we obtain
Due to(2.7),we know
Note(2.13),we obtain
Thus,the approximate solution of problem(1.1)can be given by
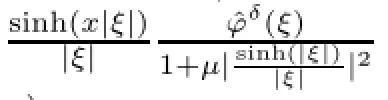
In this paper,we always assume that there holds the following the a priori bound:
where E is a positive constant.
3 Choice of Regularization Parameter and Convergence Results
In this section,we consider the a priori and a posteriori choice rule of regularization parameter,respectively,the corresponding convergence estimates are also obtained.We frst give some useful Lemmas.

Lemma 3.2For 0<x<1,we have
ProofUsing Parseval formula,the H¨older inequality and Lemma 3.1,we have
3.1 The a priori choice of the regularization parameter and the error estimate for problem(1.1)
Assume the conditions(1.2),(2.16)hold,take
then we have
Theorem 3.3Let u(x,y)given by(2.5)be exact solution of(1.1)and uμ,δ(x,y)given by (2.16)be the modifed Tikhonov regularized approximation of u(x,y).Let φδ(y)be measureddata at x=0 satisfying(1.2)and the a priori condition(2.17)holds.Then there holds the following error estimate:
ProofBecause φμ1,δ(x)is the minimizer of functional(2.6)and note(3.2),we obtain
Due to(1.2),(3.4),(2.17)and(3.5),we have
Combining(3.6),(3.7)with Lemma 3.2,we obtain the fnal estimate:
3.2 The a posteriori choice rule
In this section,Morozov’s discrepancy principle is used as a posteriori choice rule of the regularization parameter,i.e.,choosingμ=μ2as the solution of
To establish existence and uniqueness of solution for equation(3.8),we need the following lemma and remark:
Lemma 3.4Let(μ):=‖φμ,δ-φδ‖,then for δ>0,there hold
(a)(μ)is a continuous function;
(d)(μ)is a strictly increasing function.
Remark 3.5To establish existence and uniqueness of solution for equation(3.8),we always suppose 0<δ<‖φδ‖.
Theorem 3.6Assume the conditions(1.2),(2.17)hold and take the solutionμ=μ2of Eq.(3.8)as the regularization parameter,then there holds the following error estimate:
ProofSince φμ2,δ(x)is the minimizer of functional(2.6),we have
Due to(3.10),(2.17)and(1.2),we obtain
Due to(3.8)and(1.2),we get
By Lemma 3.2,(3.12)and(3.13),we obtain
The proof of Theorem 3.6.is completed.
4 Several Numerical Examples
In this section,we employ several examples to test the properties of problems(1.1).The regularized solution was computed by the Fast Fourier Transform(FFT)and IFFT techniques. We always fx 0≤x≤1,-10≤y≤10.For the exact data function,its discrete noisy version is
The function“randn(·)”generates arrays of random numbers whose elements are normally distributed with mean 0,variance σ2=1,and standard deviation σ=1,“randn(size(φ))”returns an array of random entries that is the same size as φ.In our computations,we always take N=101.The bisection method is used to solve the Equations(3.8).In order to investigate the algorithm,we evaluate the relative error defned by
Example 1It is easy to verify that the function u(x,y)=ex2-y2sin(2xy)is the exact solution of problem(1.1).The exact data functions u(0,y)=0 and φ(x)=ux(0,y)=2ye-y2.
Figs.1-3 give the numerical results computed by both a priori and a posteriori modifed Tikhonov regularization method at x=0.1,0.5,0.8 with ε=0.01,0.05 for Example 1.From these Figures,we can see that the smaller the x,the better the computed approximations.Inadditional,it can be clearly seen that the smaller the perturbation ε,the better the results. Finally,we can see that the a posteriori modifed Tikhonov regularization methods also work well for problem(1.1).
Example 2The function u(x,y)=e-|y|sinx is the exact solution of problem(1.1)with weak singularity,it satisfeswhere y=(y1,y2)∈L2(R2).
As n=2,x=0.2 and ε=0.01,Fig.4 gives the comparison of the exact and regularization solution.These fgures show that the modifed Tikhonov regularization method is also efective for solving problem(1.1)in two dimensional case.
5 Conclusion
In this paper,we proposed an efcient regularization method for solving a classical ill-posed problem-the Cauchy problem for the Laplace equation.Two diferent regularization parameter choice rules are used.For a priori choices of the regularization parameter,we obtain the H¨older type error estimates.Using the Morozov’s discrepancy principle,we give the a posteriori parameter choice rule which only depends on the measured data.For a posteriori choices of the regularization parameter,we also obtain the H¨older type error estimate.Meanwhile,several numerical examples verify the efciency and accuracy of the method.
[1]Tikhonov A N,Arsenin V Y.Solutions of Ill-posed Problems.Washington:Winston and Sons,1977
[2]Lavrent’v M M,Romanov V G,Shishat·ski?i S P.Ill-posed Problems of Mathematical Physics and Analysis. Providence RI:American Mathematical Society,1986
[3]Gorenfo R.Funktionentheoretische Bestimmung des Aussenfeldes zu einer zweidimensionalen magnetohydrostatischen Konguration.Z Angew Math Phys,1965,16:279-290
[4]Colli-Franzone P,Guerri L,Tentoni S,Viganotti C,BarufS,Spaggiari S,Taccardi B.A mathematical procedure for solving the inverse potential problem of electrocardiography.Analysis of the time-space accuracy from in vitro experimental data.Math Biosci,1985,77:353-396
[5]Johnson C R.Computational and numerical methods for bioelectric feld problems.Crit Rev Biomed Eng, 1997,25:1-81
[6]Alessandrini G.Stable determination of a crack from boundary measurements.Proc R Soc Edinburgh A, 1993,123:497-516
[7]Hadamard J.Lecture on the Cauchy Problem in Linear Partial Diferential Equations.New Haven:Yale University Press,1923
[8]Fu C L,Li H F,Qian Z,Xiong X T.Fourier regularization method for solving a Cauchy problem for the Laplace equation.Inverse Probl Sci Eng,2008,16(2):159-169
[9]Xiong X T,Fu C L.Central diference regularization method for the Cauchy problem of the Laplace’s equation.Appl Math Comput,2006,181:675-684
[10]Klibanov M V,Santosa F.A computational quasi-reversibility method for Cauchy problems for Laplace’s equation.SIAM J Appl Math,1991,51:1653-1675
[11]Latt`es R,Lions J L.The Method of Quasi-reversibility:Applications to Partial Diferential Equations.New York:Elsevier,1969
[12]Qian Z,Fu C L,Li Z P.Two regularization methods for a Cauchy problem for the Laplace equation.J Math Anal Appl,2008,338:479-489
[13]Qian Z,Fu C L,Xiong X T.Fourth-order modifed method for the Cauchy problem for the Laplace equation. J Comput Appl Math 2006,192:205-218
[14]Ang D D,Nghia N H,Tam N C.Regularized solutions of a Cauchy problem for the Laplace equation in an irregular layer:a three-dimensional model.Acta Math Vietnam,1998,23:65-74
[15]H`ao D N,Lesnic D.The Cauchy problem for Laplace’s equation via the conjugate gradient method.IMA J Appl Math,2000,65:199-217
[16]Cheng J,Hon Y C,Wei T,Yamamoto M.Numerical computation of a Cauchy problem for Laplace’s equation.ZAMMZ Angew Math Mech,2001,81(10):665-674
[17]Hon Y C,Wei T.Backus-Gilbert algorithm for the Cauchy problem of the Laplace equation.Inverse Prob, 2001,17:261-271
[18]Wei T,Hon Y C,Cheng J.Computation for multidimensional Cauchy problem.SIAM J Control Optim, 2003,42(2):381-396
[19]Vani C,Avudainayagam A.Regularized solution of the Cauchy problem for the Laplace equation using Meyer wavelets.Math Comput Model,2002,36:1151-1159
[20]Qiu C Y,Fu C L.Wavelets and regularization of the Cauchy problem for the Laplace equation.J Math Anal Appl,2008,338:1440-1447
[21]Li Z P,Fu C L.A mollifcation method for a Cauchy problem for the Laplace equation.Appl Math Comput, 2011,217:9209-9218
[22]Wei T,Zhou D Y.Convergence analysis for the Cauchy problem of Laplace’s equation by a regularized method of fundamental solutions.Adv Comput Math,2010,33(4):491-510
[23]Fu C L,Ma Y J,Cheng H,Zhang Y X.The a posteriori Fourier method for solving the Cauchy problem for the Laplace equation with nonhomogeneous Neumann data.Appl Math Model,2013,37(14/15):7764-7777
[24]Carasso A.Determining surface temperature from interior observations.SIAM J Appl Math,1982,42: 558-574
[25]Zhao Z Y,Meng Z H.A modifed Tikhonov regularization method for a backward heat equation.Inverse Probl Sci Eng,2011,19:1175-1182
[26]Fu C L.Simplifed Tikhonov and Fourier regularization methods on a general sideways parabolic equation. J Comput Appl Math,2004,167:449-463
[27]Feng X L,Fu C L,Cheng H.A regularization method for solving the Cauchy problem for the Helmholtz equation.Appl Math Model,2011,35:3301-3315
[28]Cheng W,Fu C L,Qian Z.A modifed Tikhonov regularization method for a spherically symmetric threedimensional inverse heat conduction problem.Math Comput Simul,2007,75:97-112
[29]Cheng W,Fu C L,Qian Z.Two regularization methods for a spherically symmetric inverse heat conduction problem.Appl Math Model,2008,32:432-442
[30]Yang F,Fu C L.Two regularization methods for identifcation of the heat source depending only on spatial variable for the heat equation.J Inv Ill-Posed Problems,2009,17:815-830
[31]Yang F,Fu C L,Li X X.Identifying an unknown source in space-fractional difusion equation.Acta Math Sci,2014,34B(4):1012-1024
[32]Kirsch A.An Introduction to the Mathematical Theory of Inverse Problems.Berlin:Springer-Verlag,1996
?Received August 26,2014;revised January 20,2015.The project is supported by the National Natural Science Foundation of China(11171136,11261032),the Distinguished Young Scholars Fund of Lan Zhou University of Technology(Q201015),the basic scientifc research business expenses of Gansu province college and the Natural Science Foundation of Gansu province(1310RJYA021).
?Corresponding author:Fan YANG.
 Acta Mathematica Scientia(English Series)2015年6期
Acta Mathematica Scientia(English Series)2015年6期
- Acta Mathematica Scientia(English Series)的其它文章
- REGULARITY FOR A GENERALIZED JEFFREY’S INTEGRAL MODEL FOR VISCOELASTIC FLUIDS?
- ON A CHARACTERIZATION OF THE S-ESSENTIAL SPECTRA OF THE SUM AND THE PRODUCT OF TWO OPERATORS AND APPLICATION TO A TRANSPORT OPERATOR?
- CONSENSUS ANALYSIS AND DESIGN OF LINEARINTERCONNECTED MULTI-AGENT SYSTEMS?
- ITERATIVE REGULARIZATION METHODS FOR NONLINEAR ILL-POSED OPERATOR EQUATIONS WITH M-ACCRETIVE MAPPINGS IN BANACH SPACES?
- ASYMPTOTIC STABILITY OF TRAVELING WAVES FOR A DISSIPATIVE NONLINEAR EVOLUTION SYSTEM?
- ON AN EQUATION CHARACTERIZING MULTI-CAUCHY-JENSEN MAPPINGS ANDITS HYERS-ULAM STABILITY?
