Two-phase SPH simulation of vertical water entry of a two-dimensional structure ＊

Lin Ma (馬林), Xi Zhao (趙曦), Hua Liu (劉樺)

1. Key Laboratory of Hydrodynamics (Ministry of Education), School of Naval Architecture, Ocean and civil Engineering, Shanghai Jiao Tong University, Shanghai, 200240 China

2. State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

3. College of Ocean Science and Engineering, Shanghai Maritime University, Shanghai 200135, China

Abstract: In view of the fact that the SPH model is easy to handle the flows with the free surface of large deformation, a 2-D flow induced by vertical water entry of a 2-D structure is simulated using the two-phase SPH model.The local pressure of the boundary particles is obtained by pressure of the fluid particles nearby through a modified kernel approximation.To evaluate the accuracy of the method, water entry of a 2-D symmetric wedge with fixed separation point of the free surface on the wedge surface is simulated.The pressure distribution of the wedge at the initial stage agrees well with the analytical results available.Evolution of the free surface and the air flow in the cavity induced by the water entry are obtained.A higher speed air jet is found at the neck of the cavity when the neck of the cavity becomes smaller.For the case of a horizontal cylinder entering the water with an unknown separation point of flow on the model surface, the early stage of the water entry is simulated for the rigid body with different density.Evolution of the free surface deformation of the half-buoyant cylinder and neutrally buoyant cylinder water entry is compared with the experimental data.The effects of the density ratio and Froude number on the pinch-off of the cavity are discussed.It is found that the pinch-off time remains almost constant for different density ratio and Froude number.Meanwhile, for a given Froude number, the dimensionless pinch-off depth and the location of the cylinder at the time of pinch-off increase with the density ratio.Further, for a given density ratio, these two parameters increase with the Froude number and, however, the relative cavity shape appears to be a self-similar shape when Fr≥ 8 .35.

Key words: Smoothed particle hydrodynamics (SPH), two-phase, water entry, density ratio

Introduction

Due to the complicated hydrodynamic features during the entry process, such as the deformation of free surface, evolution of the cavity region, fluid impact force and motion of the falling object, the water entry of a body has been considered as one of the challenge problems in hydrodynamics.May[1]systematically investigated the cavity-running behavior of vehicles and summarized the water entry problems.Recently, using the technology of highspeed cameras, Truscott et al.[2]designed a series of experiments to study water entry problems, including hydrophilic sphere, hydrophobic sphere, spinning ball and so on.Their experiments have shown miraculous underwater phenomenon after solid objects entering water.

Since the interactions between the fluid and structure usually lead to the large free surface deformation and wave breaking, the numerical simulation of the violent flow with the free surface belongs to one of the complicated flows for computational fluid dynamics.For example, Zhao and Faltinsen[3]used the potential flow theory to solve vertical water entry of a 2-D axisymmetric body.Wu et al.[4]used the boundary element method to compute the hydrodynamic flows associated with the water entry of a wedge.The smoothed particle hydrodynamics (SPH) method is one of the mesh-free methods.It was firstly presented to solve astrophysical problems by Lucy[5].Besides the applications of the SPH method in multi-phase flows and heat transfer, it should be mentioned that the SPH method is of great advantages in simulating the large deformation and breaking of the free surface,e.g., Liu et al.[6]and Zhang et al.[7].Oger et al.[8]developed a SPH formulation with a spatially varying resolution, based on the so-called variable smoothing length technique, to capture the violent flow with the free surface induced by water entry of a 2-D wedge.Gonget al.[9-10]implemented the two phase SPH model to simulate water entry of a wedge to study the water entry problem of a wedge entering the free surface and validated with the experimental data for the late stage of the wedge running with a cavity.

The robust treatment of solid boundary conditions is also quite important, especially for the boundaries surrounding the moving structure.The repulsive boundary, proposed by Monaghan[11], provided a simple treatment of the solid wall to prevent particle penetrations, but it could cause the pressure oscillations in the fluid region.Cummins and Rudman[12]developed the mirroring boundary to implement SPH simulation, which could be the most accurate one but it was achieved at the expense of the CPU time, and also the numerical program could become heavy for the complex boundary configurations.Gómez-Gesteira and Dalrymple[13]implemented the so-called dynamic boundary to provide an alternative way to treat the solid boundary with economic computing time.

The evolution of the cavity generated by water entry of a body has been considered as the hydrodynamic flows which follow the similarity of the Froude number in the scale of engineering structures.The difference between the water density and the density of the structures could also influence the cavity evolution for the case of free dropping test of the vertical water entry.To describe the free surface profiles caused by a cylinder dropped into calm water,Greenhow and Lin[14]presented a sequence of photographs for water entry of a half-buoyant and neutrally buoyant cylinder.Semenov and Wu[15]presented a general similarity solution for water entry problems of a wedge with its inner angle fixed and its sides in expansion with flow detachment, in which the speed of expansion is a free parameter.Kiara et al.[16]applied SPH method to simulate the water entry of horizontal cylinders with vertical impact velocity,either kept constant or freely falling, without and with spin, into quiescent water under the effect of gravity.They presented the effects of non-dimensional submergence time, Froude numbers, spin ratios and mass ratios on the flow and cavity forming stages.However,further study on the buoyant effect on the cavity evolution is needed.

In this paper, a new local pressure method is proposed which could resolve complex boundary or moving boundary conveniently.Details on the new local pressure method are discussed in later sections.A 2-D wedge water entry is simulated to validate the accuracy of the new local pressure method.The pressure distribution of the wedge at the initial stage agrees well with the analytical results.Furthermore, a study on vertical water entry of a two-dimensional cylinder with a moving curvature boundary based on the new local boundary is investigated.The first case is the test example of constant speed.The SPH results are compared with experimental results in literature.The second case is the impact of a horizontal free-motion cylinder which means the fluid-structure coupling should be considered.The horizontal cylinder has only one degree of freedom, namely the vertical motion.The drag force on the cylinder is obtained by the integration of the pressure of the particles on the cylinder.Both of the half-buoyant cylinder and neutrally buoyant cylinder are simulated.The evolution of the free surface and the depth of penetration computed by the SPH model are compared with experimental and other numerical results.Then,the effects of the density ratio and Froude number on the pinch-off time, pinch-off location and the shape of the cavity are discussed.

1.SPH formulation

1.1 Governing equations

The flow is assumed to be non-viscous, namely ignoring the shear stress of the fluid.Both water flow and air flow are simulated.The governing equations are the Euler equations formulated as follows:

whereρrefers to fluid density,trefers to time,urefers to the velocity vector of fluid particles,grefers to the gravitational acceleration,prefers to pressure, D/Dtrefers to the material derivative and? is the gradient operator.

The SPH formulation of governing equations can be written as:

whereWrefers to an interpolating kernel function,superscriptsaandbrefer to different particles,is an artificial viscosity term.In this paper, a spline function proposed by Monaghan and Lattanzio[17]is adopted:

wheread=2/3h, 1 0/7 πh2, 1/πh3for 1-D, 2-D, 3-D condition,R=|r′-r|h,his the smoothing length.

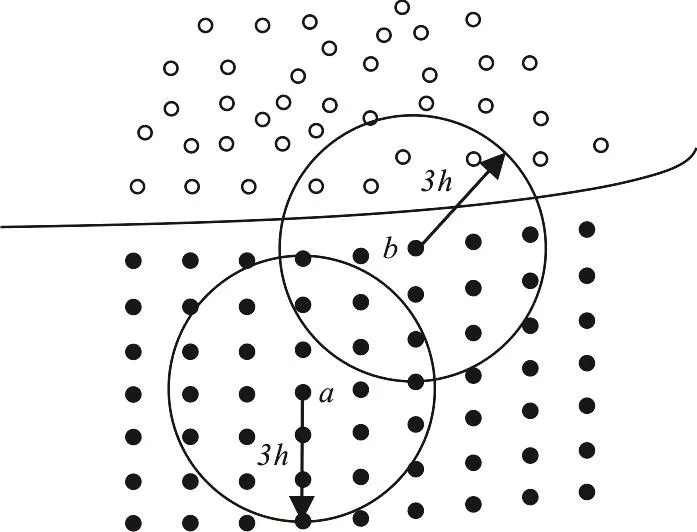
Fig.1 Water (black) and air (white) particles near the interface

Two different particles are used in the water and air flow, namely water particles and air particles.The particles 3haway from the interface, are the same species in the support domain, as shown in Fig.1.When the particle is close to the interface enough, like particleb, both water particles and air particles are involved in the support domain.For particleb, the momentum equation can be written as

where subscriptiandjrepresent water particle and air particle,N1andN2are the number of water particle and the number of air particle in the support domain of particleb.

For classical SPH method, the pressure of the fluid particles is calculated through an equation of state as follows

1.2 Boundary condition

If a functionf(x) is sufficiently smooth in its definition domain, it can be expressed as Taylor series expansion in the vicinity ofxi

Multiplying by a smoothing functionWboth sides of the above equation and integrating over the support domain, we can obtain the following equation

If we replace the functionf(x) as the pressure function of boundary particles in Eq.(10), then

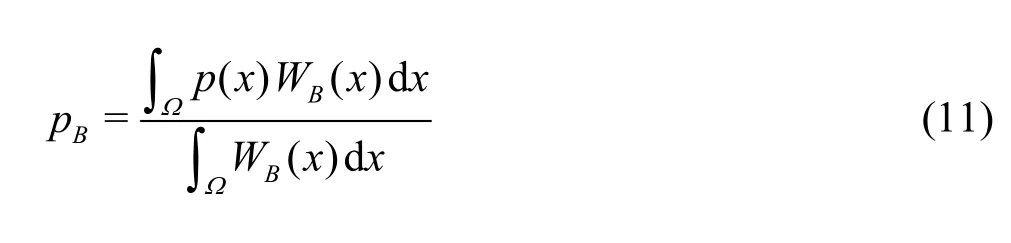
which can be written as particle approximation as

Based on the new local boundary treatment,problems with complex boundary or moving boundary can be solved.In order to validate the new approach, a 2-D cylinder water entry is simulated.

2.Validation

2.1 Water entry of a 2-D wedge

In this section, a 2-D symmetric wedge water entry problem is simulated.The wedge is assumed to enter water vertically at a constant speed of 1 m/s.The deadrise angle of the wedge is 15°.The sketch of the simulation is shown in Fig.2.

Fig.2 Sketch of vertical water entry of a 2-D wedge (β is the deadrise angle, v0 =1m/s)

Fig.3 Pressure distributions on the wedge (t=0.004s)

The pressure distribution of the wedge at the initial stage is shown in Fig.3, whereyrefers to the distance between the lowest point of the wedge and the initial free surface.The two-phase results have been compared with the analytical results obtained by Zhao et al.[3].

The evolution of the cavity induced by the impact is shown in Fig.4.At the first stage, a splash appears in a very short time after the water entry.As the wedge descending, the water is forced outward along the wedge?s equator.The expansion of the water is resisted by hydrostatic pressure.Then the cavity begins to shrink.Eventually, the cavity collapses until the moment of deep seal.

Fig.4 Evolution of the free surface

The velocity field of the air flow in the cavity is shown in Fig.5.It is found that the speed of the air in the cavity?s neck becomes higher when the cavity begins to shrink.From Fig.6, the speed of the air flowing through the neck can be obtained as

wheredis the width of the neck,Nairrefers to the number of the air particles in the cavity below the neck.

Fig.5 Velocity distribution at t =0.236s

The correlation between the dimensionless speed of the air flowing through the neck and the Froude number which is defined asshown in Fig.7.It is obvious that the air maintains low speed whenFr′≤13.WhenFr′≥ 26, the dimensionless speed increases rapidly and attains 182 whenFr′= 1 00.The details can refer to Ma and Liu[18].

Fig.6 Sketch of the air flowing through the neck

Fig.7 The development of the di me nsionless air spe ed a t the neck (un is the speed of the airflowing through the neck,v0 is the speed of the wedge and , d is the width of the neck)

3.Numerical results and discussion

3.1 Water entry of a horizontal cylinder

In this section, classical problems of a horizontal circular cylinder water entry are solved by using the SPH model with the new boundary treatment presented previously.First of all, a test case with constant speed is simulated.The results are compared with the experimental data obtained by Miao[19].Actually,water entry problem with constant speed can be seen as a moving boundary problem.The drag force of the cylinder when it penetrates the water is obtained by the integration of the pressure of the boundary particles on the cylinder.Furthermore, a test case of free motion is simulated.In this condition, unlike constant speed case, fluid-structure coupling should be considered.The motion of the cylinder is governed by its gravity and the drag force.The cylinder has only one degree of freedom, which means only the vertical motion is allowed.

Firstly, a horizontal circular cylinder is forced into an initially calm water surface with a constant vertical velocityv0.The SPH model is compared with the water entry tests conducted by Miao[19].The initial geometry of the computational domain is shown in Fig.8.

Fig.8 Sketch of the horizontal cylinder water entry

Fig.9 Non-reflection boundary treatment

As shown in Fig.8, the water depth is 1 m and the diameter of the cylinder is 0.125 m.The cylinder enters into the water surface with a constant speed of 0.64 m/s.In our simulation, the computational domain could not be as large as the experiment of Miao,therefore, the length of the tank is set to be 1.6 m.In order to remove the influence of wall effects, a sponge layer is placed in the region within a certain distancedfrom the solid boundary to absorb the sound wave as shown in Fig.9[9].We use the non- reflection boundary treatment to prevent the sound wave from disturbing pressure field.In the sponge layer, the density of the fluid particles is obtained through

where the coefficient of wave absorptionθtakes the form

where

wheredis the width of the sponge layer,ypis the coordinate of fluid particles,ywis the coordinate of the boundary of the sponge layer.

The initial average distance of the particles is 0.0025 m, and the total number of the fluid particles is 400×640.The non-dimensional impact force is defined as

whereFyis the total vertical hydrodynamic force reduced from the water entry including the buoyancy force,ρ, the speed of the cylinder is a constantv0=0.64m/s ,Dis the diameter of the cylinder.Fyis obtained by the integration of the pressure of particles on the cylinder

Fig.10 Time history of slamming coefficient during water entry process ( t* =2 v0 t/D)

Att=0, the cylinder is forced into the calm water surface.The slamming coefficientCsas a function of non-dimensional time is shown in Fig.10.The maximum impact pressure occurs at the instant when the cylinder impacting the free surface.From the figure, we can see the slamming coefficient decreases as the cylinder penetrates the water before 2v0t|D= 0.4(t= 0.039s).After 2v0t|D= 0.4, the slamming coefficient increases because the wet surface increases.At the time on 2v0t|D= 3.0(t=0.30s), the cylinder is totally wetted, and the slamming coefficient tending towards stability.The contribution of the buoyancy to the slamming coefficient is defined as

where/(gD) .For this case in the paper,Csb=4 .71.As shown in Fig.10, the slamming coefficient obtained by SPH model agrees well with the experimental results.

Secondly, the cylinder is considered as dropped into the calm water with free motion.Two kinds of cylinder will be simulated, one is half-buoyant, and the other is neutrally buoyant.The diameter of both cylinders is 0.11 m.The SPH simulation results are compared with the experiments conducted by Greenhow and Lin[14].

For the case of constant speed, the cylinder is a moving boundary actually, but for the free motion,fluid-structure coupling should be considered.With the new local boundary method, the pressure on the cylinder could be obtained conveniently by Eq.(12).The drag force is obtained by the integration of pressure of the particles on the cylinder as Eq.(15).

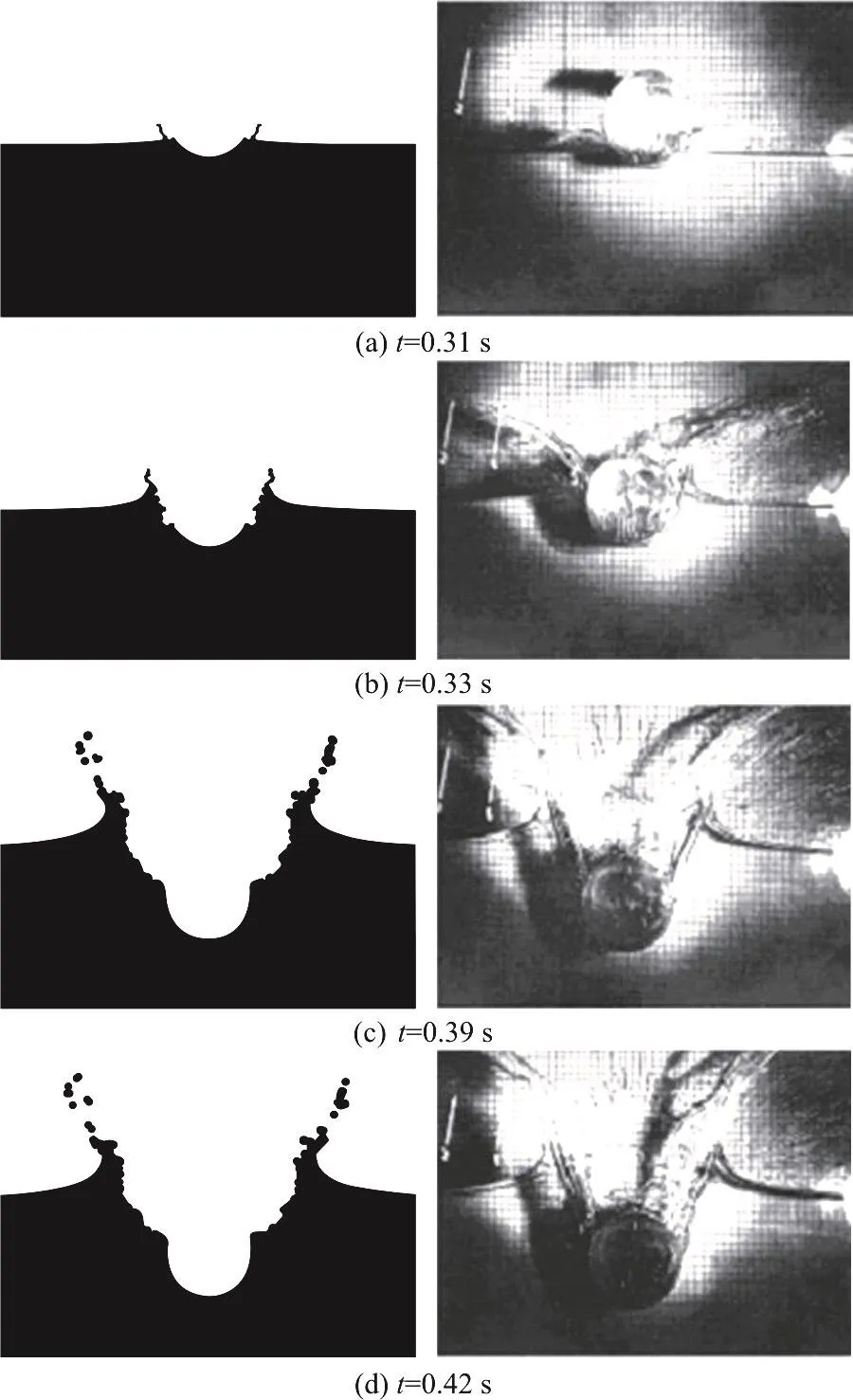
Fig.11 Evolution of the free surface deformation for the case of a half-buoyant cylinder and initial speed 3.13 m/s.Left panel: SPH simulations, Right panel: high-speed images by Greenhow and Lin[14]

The simulation starts from the moment when the horizontal cylinder impacts the calm free surface.In the experiment of Greenhow and Lin, the cylinder is released from a height of 0.50 m between the lowest point of the horizontal cylinder and the calm free surface.The initial velocity of the cylinder is set toThe free fall time ist0≈v0|g≈0.139s when the lowest point of the cylinder impacts the free surface.

Figure 11 illustrates the evolution of the free surface of a half-buoyant cylinder water entry.As shown in Fig.11(a), we can see two jets form from the contact points of the cylinder and the liquid.As one can see, the SPH model can deal with the problem of large deformation well.

Figure 12 shows the time series of the penetration depth of the half-buoyant cylinder.The results of the SPH model are compared with the experimental data and computed values by the CIP method[20].Satisfactory agreements can be obtained for the half-buoyant cylinder.As shown in the figure, at the first stage whent＜0.35s, the penetration depth is linearly proportional to the time because the drag force is basically equal to the gravity.As the cylinder descends, the wet surface increases.Finally, the drag force is greater than the gravity and the acceleration of the penetration depth decreases.

Fig.12 Time history of penetration depth during a half-buoyant cylinder water entry

The evolution of the free surface of a neutrally buoyant cylinder is shown in Fig.13.Similar to the half-buoyant cylinder, two jets form when the cylinder impacts the free surface.As the cylinder descends, an axisymmetric cavity appears below the free surface.The open cavity adjoins the cylinder near its equator,and it has a similar size with the cylinder.As the horizontal cylinder penetrates the water, its momentum is transferred to the fluid by forcing it outward radially, as shown in Fig.13(b).The expansion of the cavity is resisted by the hydro-static pressure and then the direction of the radial flow is reversed which makes the cavity begin to shrink as shown in Fig.13(c).Eventually, the cavity collapses below the surface which is called deep-seal.When the cavity collapses, one jet forms and moves up towards the free surface as shown in Fig.13(d).

Figure 14 shows the time history of submergence depth of the neutrally buoyant cylinder.The experimental datum tagged by a question mark att=0.34s is questionable because this datum deviates from other data.As shown in the figure, the SPH results agree well with the CIP results and experimental data.

Fig.13 Evolution of the free surface deformation for the case of a neutrally buoyant cylinder and initial speed 3.13 m/s.Left panel: SPH simulations, Right panel: high-speed images by Greenhow and Lin[14]

3.2 Effect of the density ratio on pinch-off

In this section, the effect of density ratio and Froude number on pinch-off is investigated numerically.The density ratio is defined asand the Froude number is defined as

Fig.14 Time history of penetration depth during a neutrally buoyant cylinder water entry

Fig.15 Dimensionless pinch-off time as a function of the Froude number for different density ratios ( r= ρc|ρwater)

The depth of the water is 1.40 m and the diameter of the cylinder is 0.11 m.The horizontal cylinder is dropped into the water at initial speed at the range of 1-5 m/s.The Froude number values 0.93 to 23.20.The density ratio is set at the range of 1-6, say from the small density to the large density of the cylinder.The related parameters for the numerical experiments are summarized in Table1.In Fig.15, we plot data for the dimensionless pinch-off time as a function of the Froude number for different density ratio.It is obvious that the pinch-off time is independent of the Froude number for any density ratio.The pinch-off time is about 250 ms after impact.Figure 16 shows the dimensionless pinch-off locationh*and the depth of the center of the cylinder at the time of pinch-offH*as a function of the Froude number for different density ratio, whereh*=h|D,H*=H|D.In Fig.16, (a), (b) illustrate thath*andH*increase as the Froude number.For the same Froude number, a heavy cylinder could generate a big cavity in the process of water entry.In the limit of 0.93≤Fr≤23.20 and 1≤r≤6,h*andH*can scale linearly withForh*,c( 1)=0.80,ForH*,c(1)=Fig.16(c)shows thath|His almost a constant 0.3 for different density ratio.In summary, both Froude number and density ratio can alter the values ofh*andH*, but neither of them can alter the values ofh|Hevidently.

Fig.16 The relationships between the characteristic coefficient and the Froude number.(a) The dimensionless pinchoff depth.(b) The dimensionless depth of the center of cylinder at the time of pinch-off.(c) The scaled pinchoff depth h|H

Table1 Parameter values of water entry

Fig.17 The water entry cavity shapes for different Froude numbers a nd different density ratios.(a) Computed cavity shape for different density ratios at Fr = 23.2 .(b)Computed cavity shape for different Froude number at r = 2 .(c) Computed cavity shape scaled with the length of the cavity for different Froude number at r= 2

Computed cavity shapes are shown in Fig.17.The origin (x,y) =(0,0) corresponds to the location of the pinch-off point.In the first figure, the correlation between cavity shape and density ratio is shown in the condition ofFr= 23.2.Forr=1, the cavity shape is small because the speed of the cylinder decays sharply after the cylinder water entry.For bigger density ratio, the effect of the gravity could provide driving force to the cylinder, and makes the cavity shape longer and wider at the moment of pinch-off.In the second figure, the cavity shapes are scaled withτv0, in whichτrepresents pinch-off time.Five cavity shapes show different Froude number in the condition ofr=2.Based on this figure, the third figure is obtained.In the figure,ymaxis the length of the cavity.It is clearly shown that, the relative cavity shape is slimmer and forms to a more streamlined structure as the Froude number increases.Notably, the cavity shape appears to be a self-similar shape whenFr≥ 8 .35.

4.Conclusions

Vertical water entry of a 2-D structure is simulated based on the two-phase SPH model.A new local boundary treatment method in the framework of the coupling boundary method is presented.The method is derived by a corrective kernel approximation and validated by a 2-D symmetric wedge water entry.The pressure distribution of the wedge at the initial stage agrees well with the analytical results.Based on the results of 2-D wedge water entry, a high speed air jet is found when the neck area of the cavity becomes small.

In order to verify the capability of the new method for complex boundary, horizontal cylinder water entry problems are simulated.First of all, test case of constant speed is calculated.In this condition,the cylinder is actually treated as a moving boundary.The evolution of the free surface and the slamming coefficient during cylinder water entry obtained through SPH model are compared with the experimental data.Secondly, test cases with free motion are simulated.In this situation, fluid-structure coupling is considered.The motion of the cylinder is controlled by the drag force and the gravity and the flow field is influenced by the cylinder water entry.A half-buoyant cylinder and a neutrally buoyant cylinder are simulated by the new method.It is found that the evolution of the free surface and the time history of penetration of depth agree well with the measured data available.

The effect of the density ratio and Froude number on the pinch-off is studied.It is shown that the dimensionless pinch-off depth and the dimensionless submerged depth of the center of cylinder at the time of pinch-off increase as the density ratio for the same ratio increases, however the ratio of the pinch-off depth and the corresponding submerged depth remains a constant.For a given Froude number, larger density ratio could make the pinch-off depth and the corresponding submerged depth greater.The effects of Froude number and density ratio on the pinch-off depth and the submerged depth are obtained through numerical experiments.For a given density ratio, the relative cavity shape becomes slimmer as the Froude number increases and appears to be a self-similar shape for the cases of greater Froude number.