一維線性Klein-Gordon方程Neumann邊值問題的高階差分格式
盛秀蘭郝宗艷吳宏偉
(1.東南大學數學學院,江蘇南京 210096)
(2.江蘇開放大學通識教育學院,江蘇南京 210036)
1 引言
本文研究如下一維非線性Klein-Gordon方程Neumann的邊值問題的數值解
其中α>0為常數,f(x,t),g(u)為滿足相容性條件的光滑函數.
Klein-Gordon方程是相對論量子力學和量子場論中用于描述零自旋粒子的自由運動方程,關于它的數值解法已有不少研究結果.文獻[1]基于樣條基函數提出了一個數值格式;四階緊格式在文獻[2]中進行了研究;基于變分迭代法的數值格式及邊界元方法可參見文獻[3,4];在文獻[5]中導出了以三層樣條差分格式逼近非線性Klein-Gordon方程;無界域上的問題的數值研究可參見文獻[6];文獻[7]中提出了一個基于有限差分和匹配法的新的數值格式;而文獻[8]提出了微分積分法.所有這些文獻中的研究都是針對Dirichlet邊界條件,對于Neumann邊界條件下的高階差分格式還沒有很好的結果.近年來,具有Neumann邊界條件的熱方程的高階差分格式已有一些研究結果如文獻[9–11].文獻[12]研究了Cahn-Hilliard方程Neumann邊界條件下的三層線性化緊格式;文獻[13]中建立了哈密爾頓非線性波方程Neumann邊界條件下的高階顯格式,該方法空間方向基于緊格式,時間方向基于Runge-Kutta-Nystrom方法.通過分析以上文獻,了解到Klein-Gordon方程Neumann邊值問題的無條件穩定的高階差分格式,目前還沒有這方面的結果,其主要困難是邊界點的處理.本文利用Klein-Gordon方程及邊界條件可得到在邊界處的三階導數和五階導數的函數值,從而建立邊界點和內點處的兩點和三點緊差分格式,構造一個緊格式,并證明差分格式關于時間2階收斂,關于空間4階收斂.
2 記號及引理
設問題(1.1)–(1.3)存在光滑解u,記?=[a,b]×[0,T],本文假設
H1:u∈C(4,3)(?),且存在常數C0,使?(x,t)∈(?)有
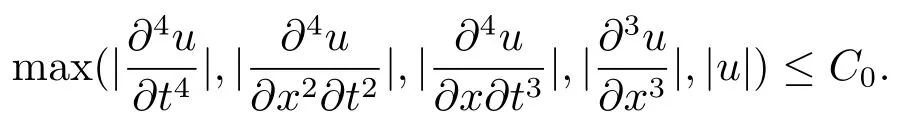
H2:函數g一階可導,且存在正常數C,使得當|s|≤C0+1時,有
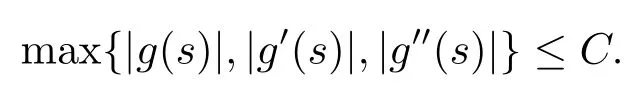
H3:?(x,t)∈?,且存在常數C1,使.
由(1.1)式中的方程可得
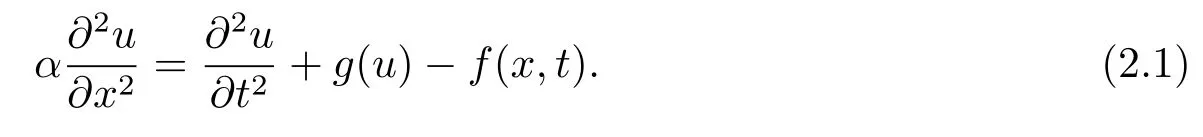
將(2.1)式兩邊關于x的k(k=3,4,5)階導數,且由邊界條件(1.3)可得
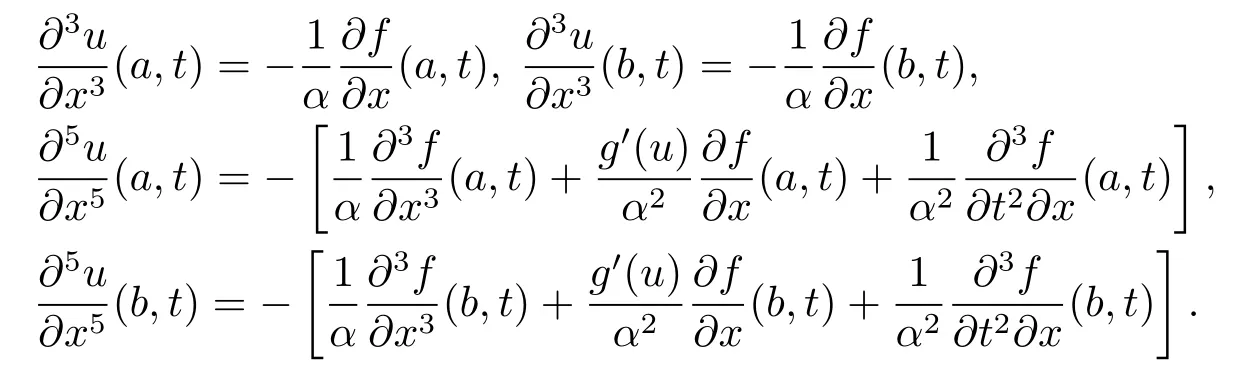
取正整數m,n,記空間和時間步長分別為,記x=a+ih,0≤i≤m,itk=kτ,0≤k≤n.定義
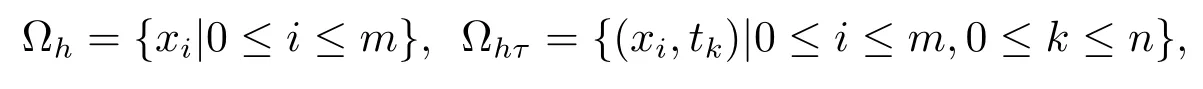
稱(xi,tk)為節點,并設為?hτ上的網格函數,引進下面的記號
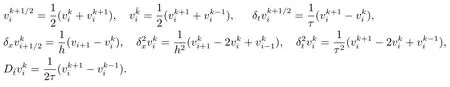
記Vh={v|v={vi|0≤i≤m}為?h上的網格函數},設v∈Vh,引進下列網格函數的模與半模
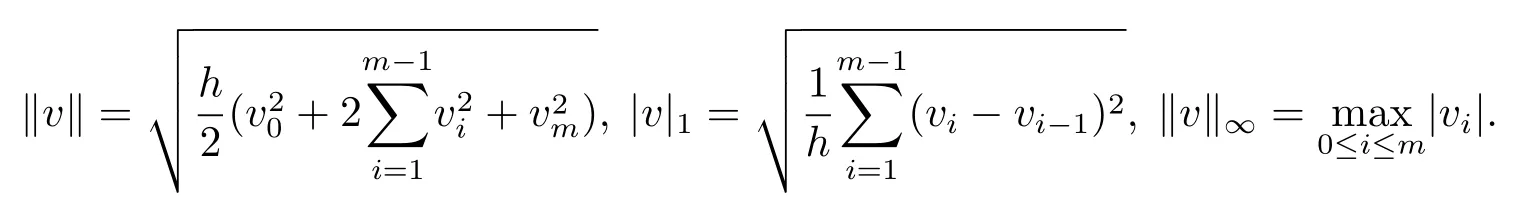
引理2.1[3]記ζ(s)=(1?s)3[5?3(1?s)2],s∈[0,1].
(1)若g(x)∈C6[x0,x1],則有
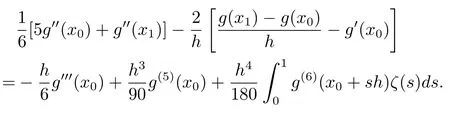
(2)若g(x)∈C6[xm?1,xm],則有
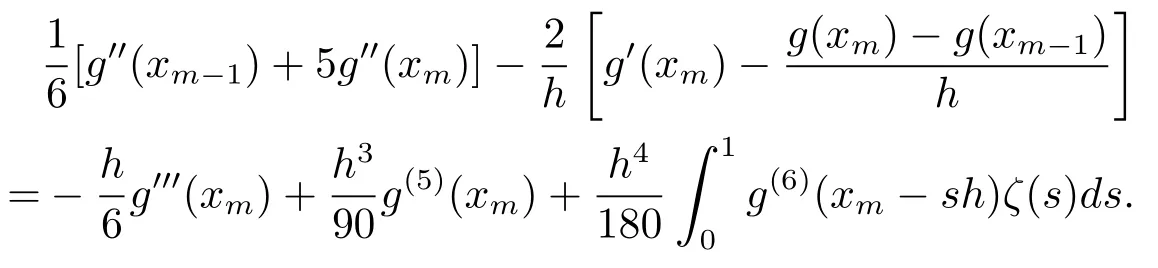
(3)若g(x)∈C6[xi?1,xi+1],1≤i≤m?1,則有
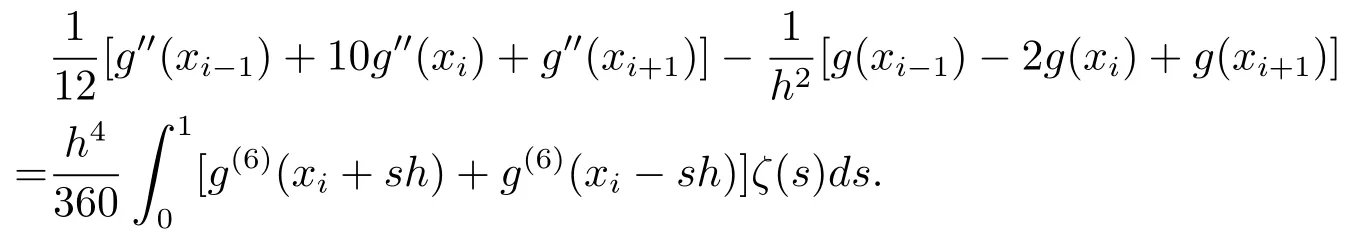
引理2.2[5]設v∈Vh,則有,且對任意ε>0,有
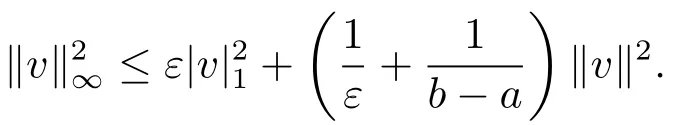
引理2.3[14]設h和c為兩個常數,且h>0,若g(x)∈C2[c?h,c+h],則有

引理2.4[15]設為?hτ上的網格函數,則
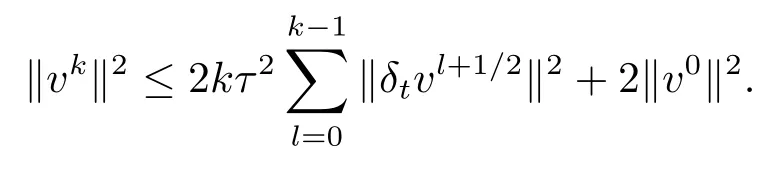
引理2.5設為?hτ上的網格函數,記
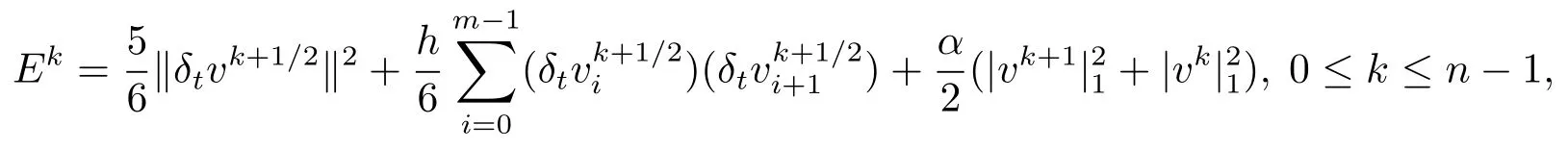
則當0≤k≤n?1時,有
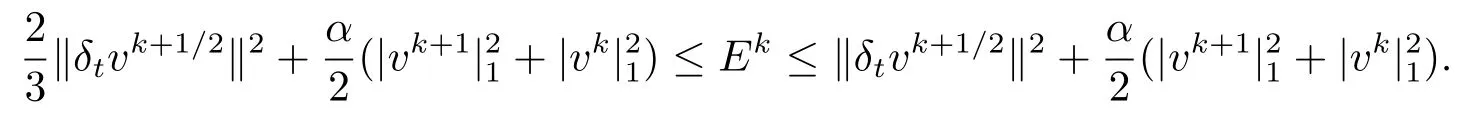
證由不等式
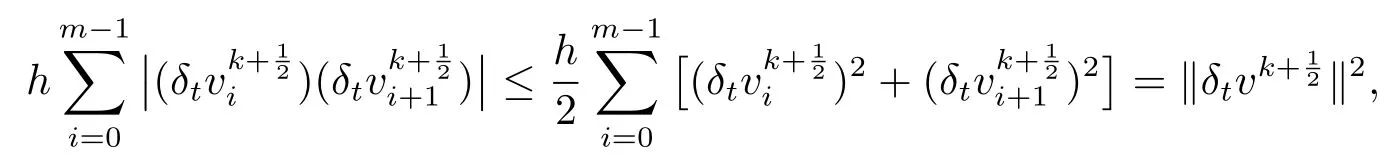
易得引理2.5.
3 差分格式的建立
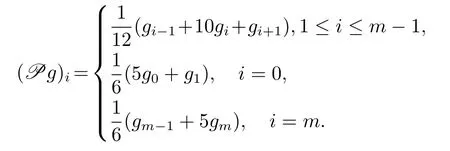
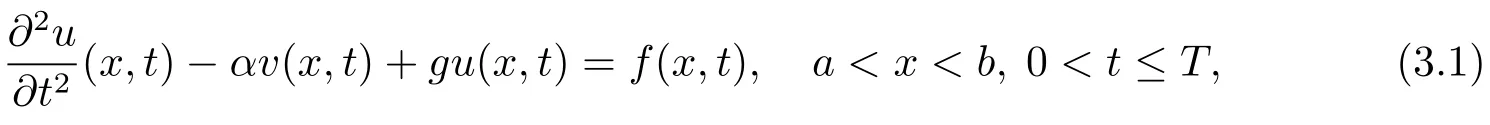
在結點(xi,tk)處考慮方程(3.1),并對兩邊作用算子P,且1≤i≤m?1,0≤k≤n?1,可得
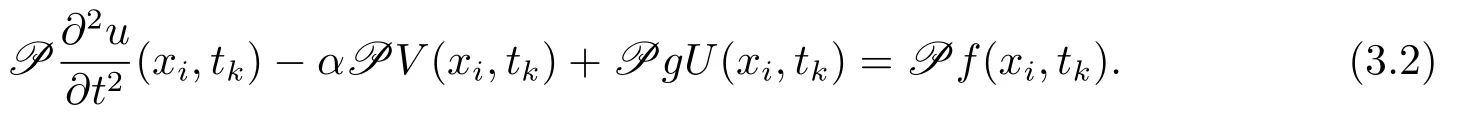
根據引理2.1,邊界條件及作用算子P可得
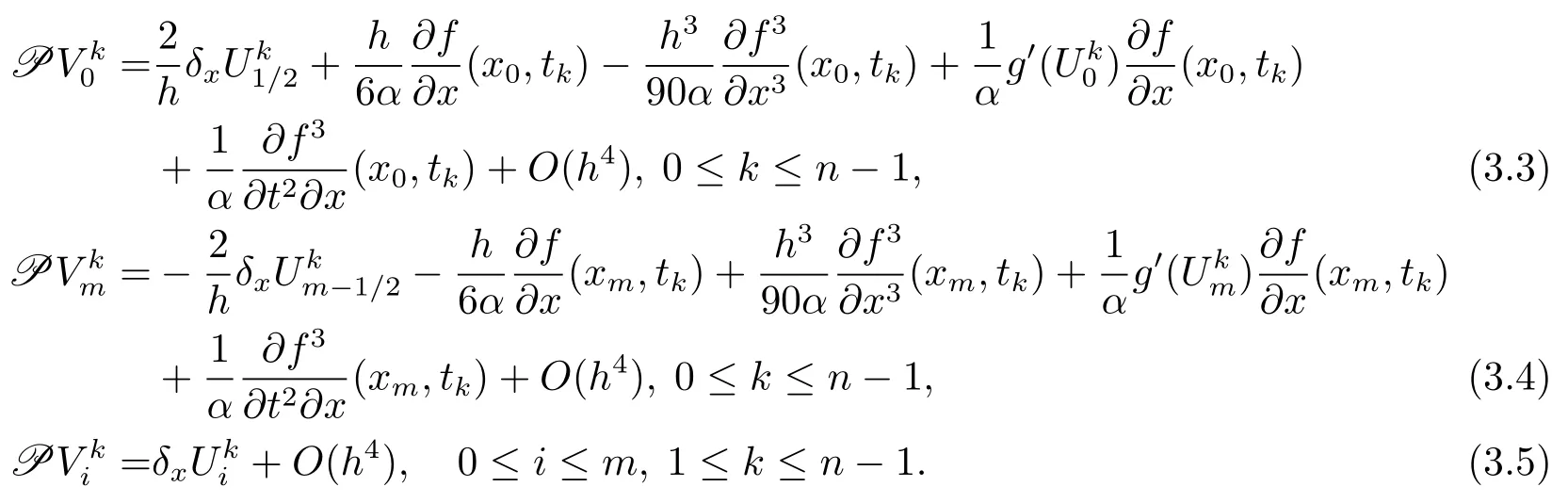
由Taylor展開知
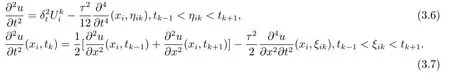
將(3.6)–(3.7)式帶入到(3.2)式,且0≤i≤m?1,0≤k≤n?1,得到
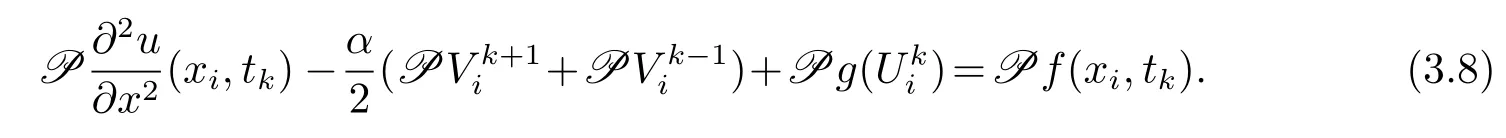
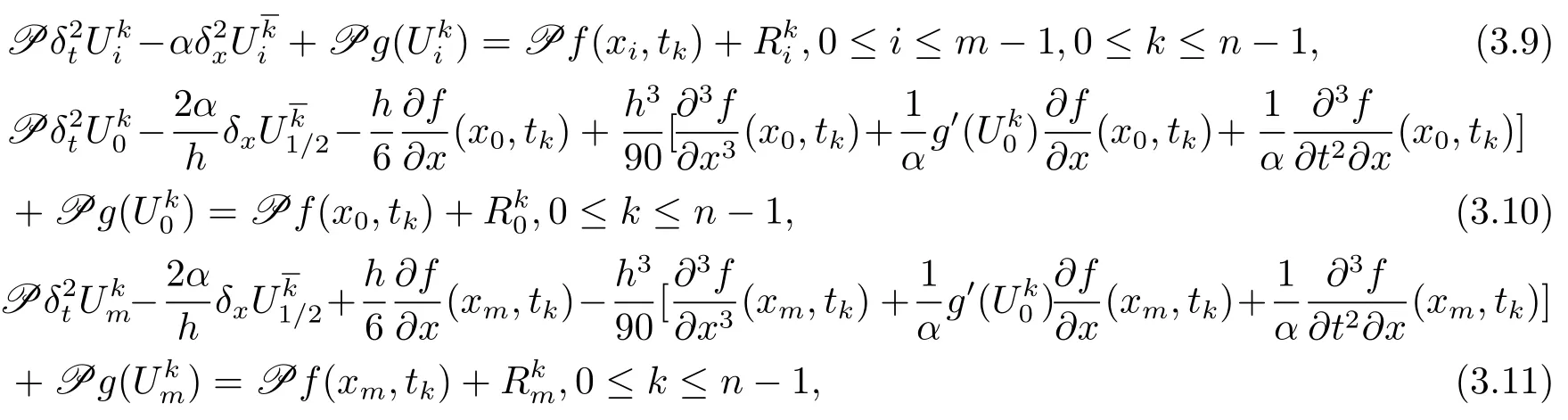
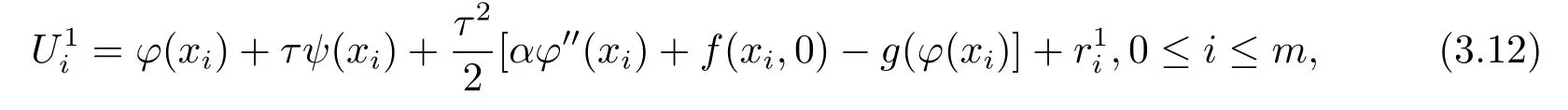
其中
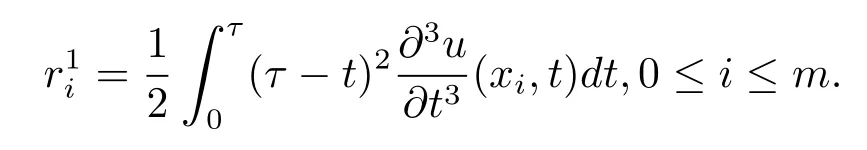
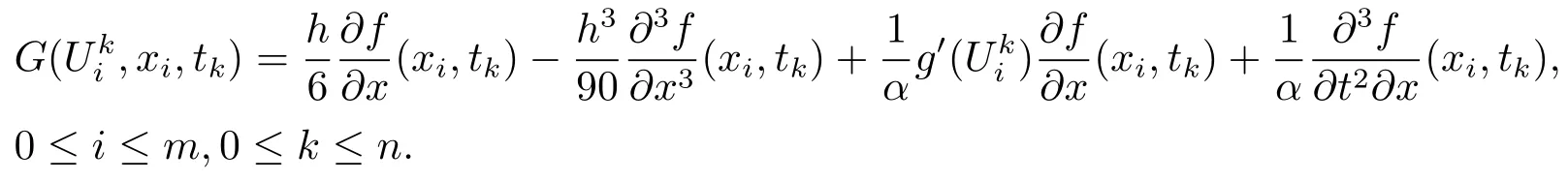
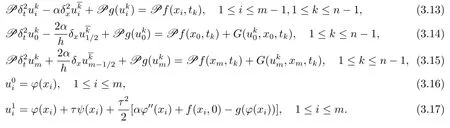
4 差分格式的收斂性
定理1設u(xi,tk)是問題(1.1)–(1.3)式的解,是差分格式的解(3.13)–(3.17)的解,記,則當時,有
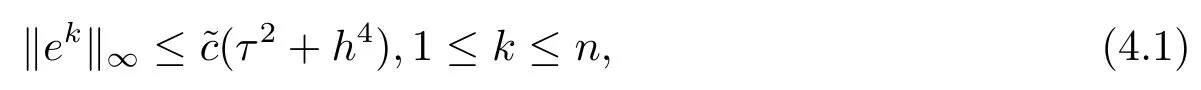
其中
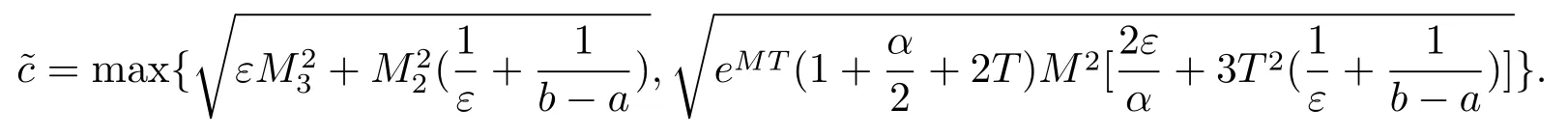
證將(3.9)–(3.12)式分別與(3.13)–(3.17)式相減,且1≤k≤n?1,得到誤差方程
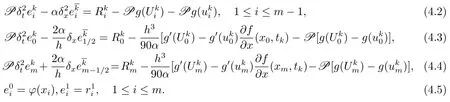
令
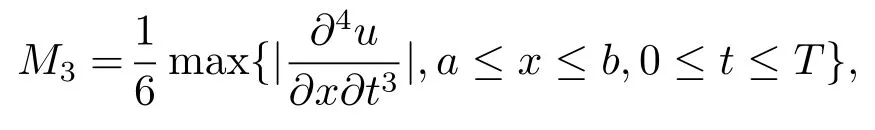
則有
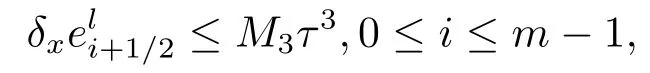
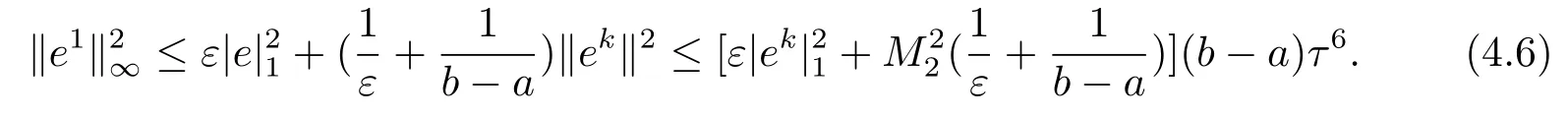
顯然,(4.1)式對于k=1成立,現假設(4.1)式對于1≤k≤l成立,其中1≤l≤n?1.下面證明(4.2)式對k=l+1也成立,用,分別乘方程(4.2)–(4.4)三式,并關于i從1到m?1求和,且將三式相加可得J1+J2=J3,其中
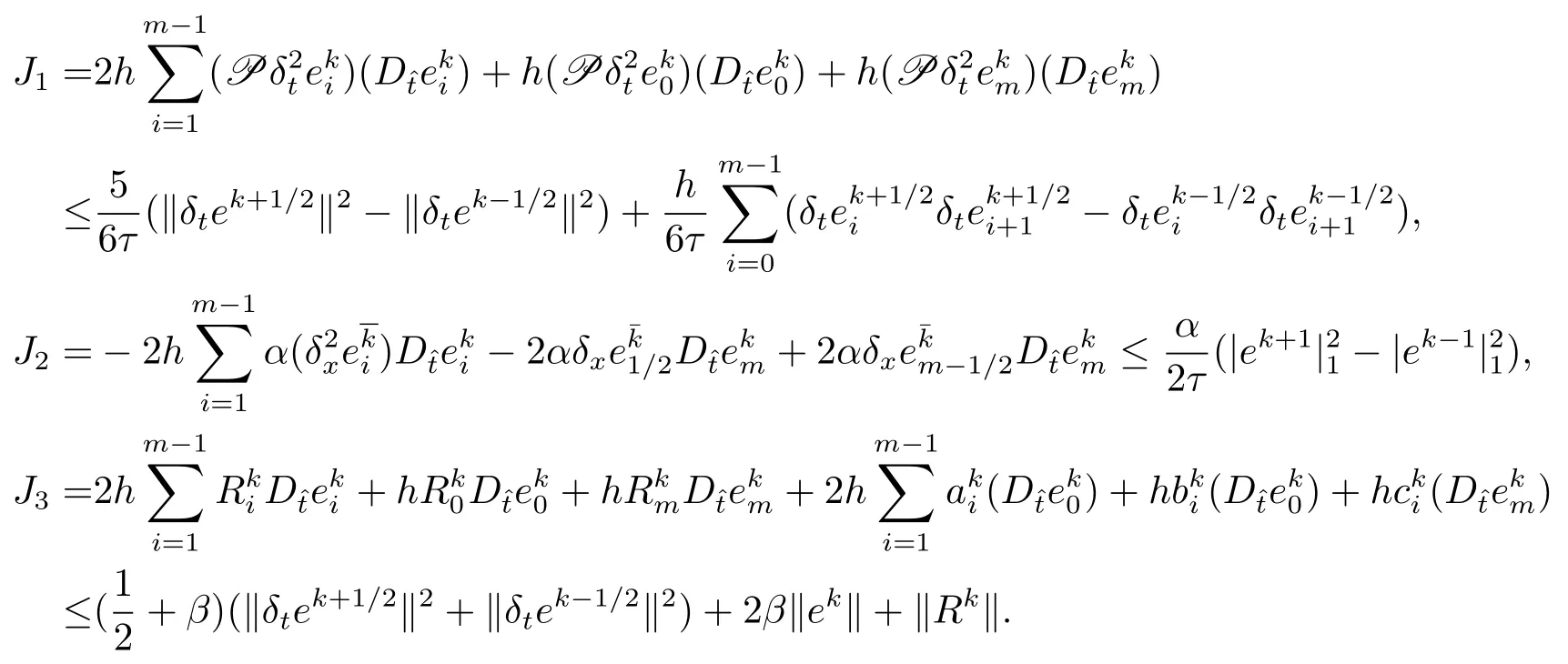
上述β為常數,其中如下
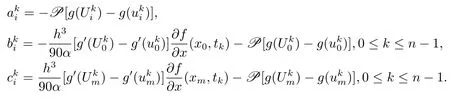
令
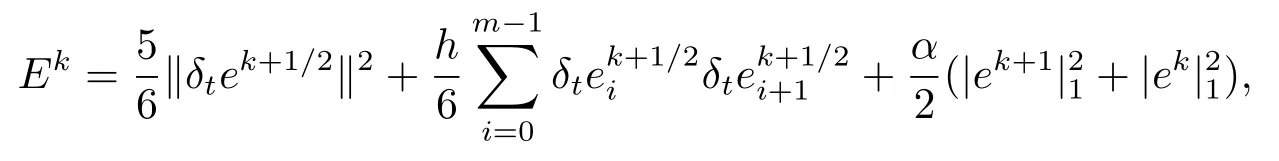
則J1+J2=J3可寫為
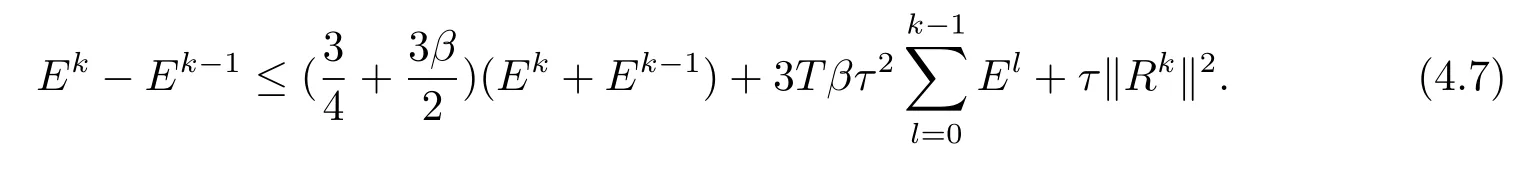
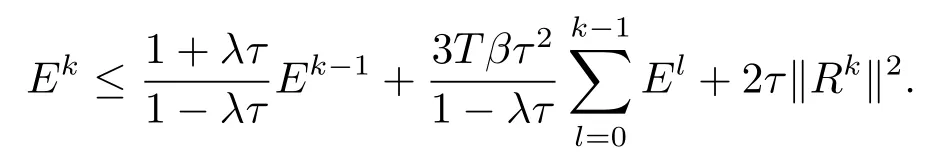
令Fk=max(Ek,Ek?1,Ek?2,···,E1,E0),則有
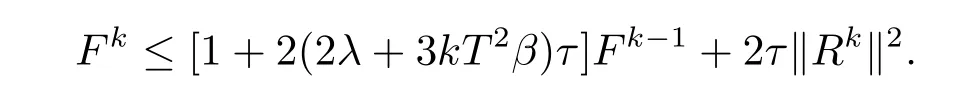
記M4=2(2λ+3kT2β),M4為正整數,故Fk≤(1+M4τ)Fk?1+2τkRkk2,由 Granwall不等式可得到
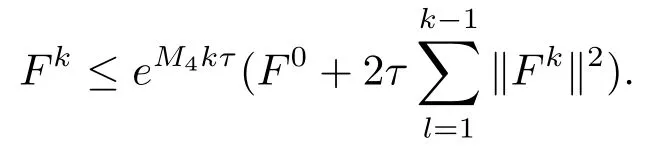
由Fk的定義可知F0=E0,則有
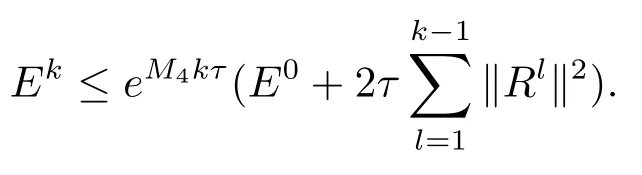
取M=max(M1,M2,M3,M4),并由引理2.5可得
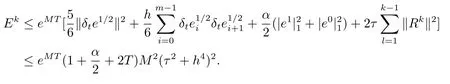
由此可得
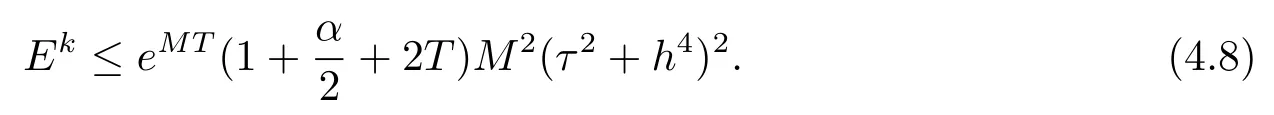
由引理2.4和引理2.5可知
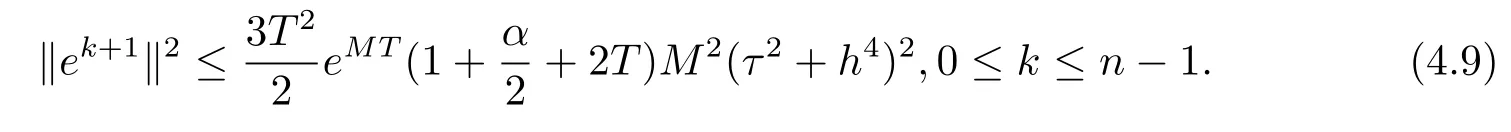
由(4.8)–(4.9)兩式和引理2.2可知,對于任意的ε>0,有
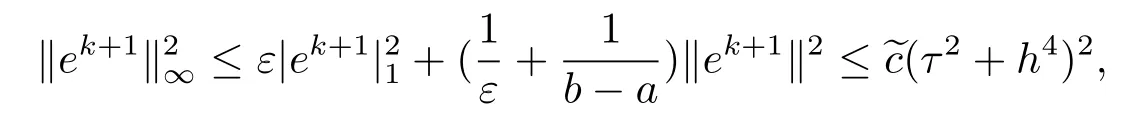
5 差分格式的穩定性
類似討論差分格式的收斂性可以得到差分格式(3.13)–(3.17)式關于初值的穩定性.
定理2設分別是差分格式(3.13)–(3.17)的解,記,假設條件H1,H2,H3成立,則當h,τ充分小時,且 1≤k≤n?1時,有
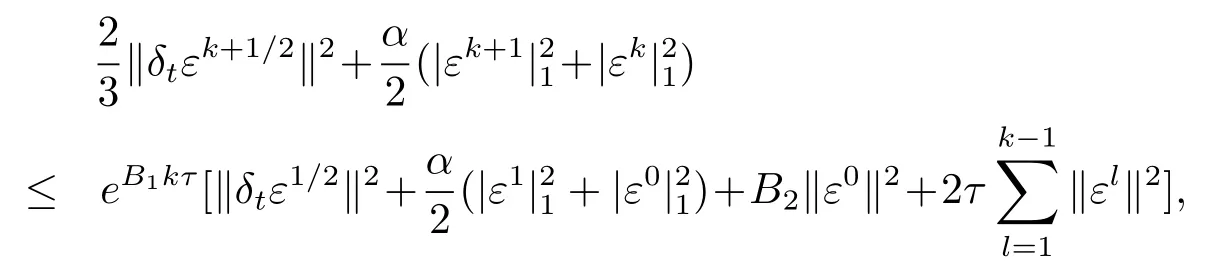
且B1,B2是與h,τ無關的正的常數,證明略.
6 數值試驗
本節利用構造的差分格式(3.13)–(3.17)計算下面的定解問題
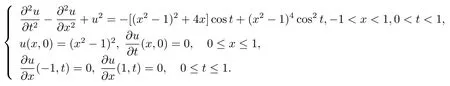
該問題的精確解為u(x,t)=(x2?1)2cost.計算結果見表6.1和表6.2.表6.1給出了在不同步長時某些節點處的誤差,表6.2給出了不同步長時數值解的最大誤差和誤差比,其中
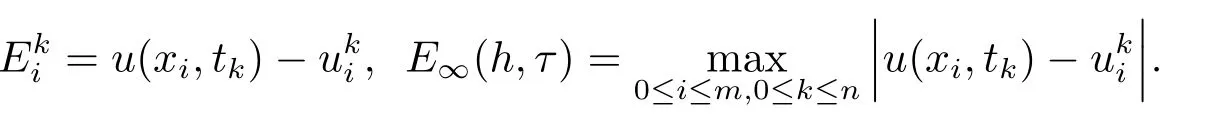
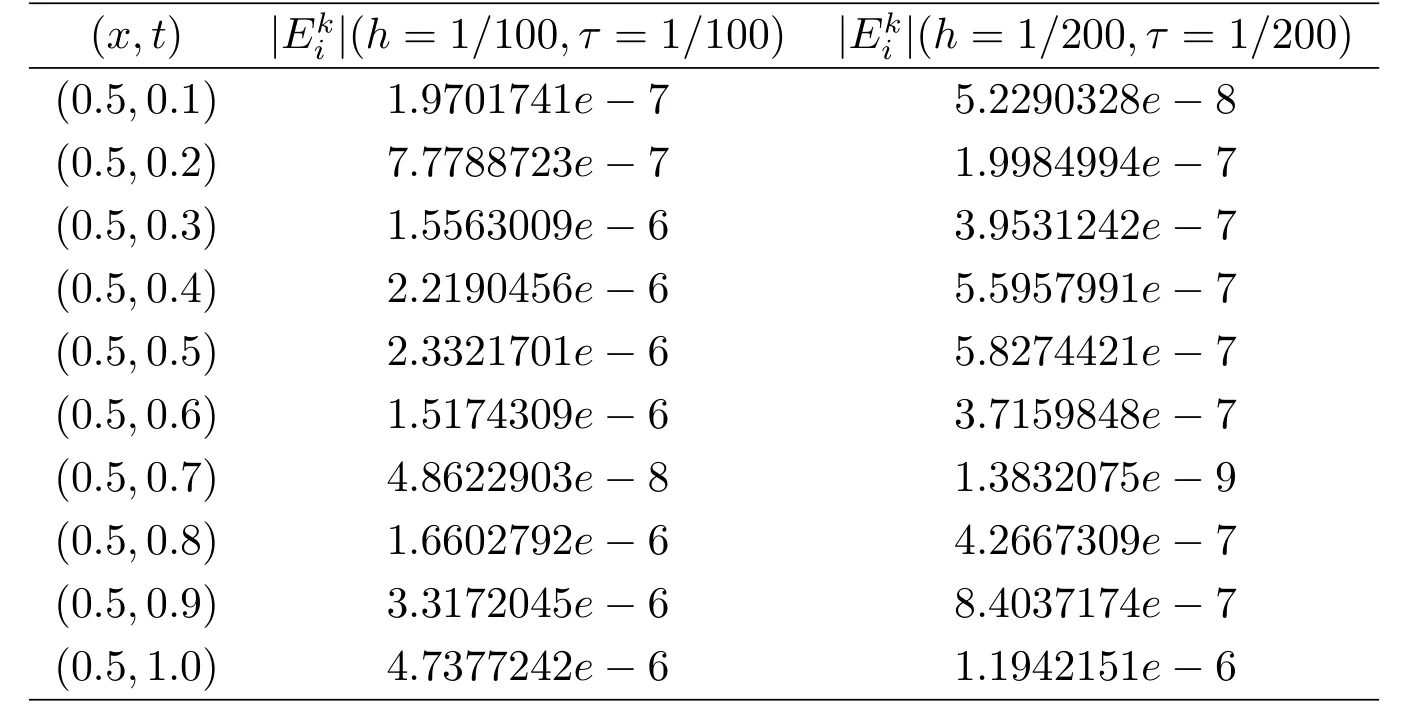
表6.1:部分結點處數值解的誤差

表6.2:不同步長時數值解的最大誤差和誤差比
由表6.2可以看出,差分格式在無窮范數下的收斂階為O(τ2+h4),這和理論分析結果一致.

