An Approach to Formulation of FNLP with Complex Piecewise Linear Membership Functions
An Approach to Formulation of FNLP with Complex Piecewise Linear Membership Functions
WEN Bo (聞博) and LI Hongguang (李宏光)*
School of Information Science and Technology, Beijing University of Chemical Technology, Beijing 100029, China
Traditionally, extra binary variables are demanded to formulate a fuzzy nonlinear programming (FNLP) problem with piecewise linear membership functions (PLMFs). However, this kind of methodology usually suffers increasing computational burden associated with formulation and solution, particularly in the face of complex PLMFs. Motivated by these challenges, this contribution introduces a novel approach free of additional binary variables to formulate FNLP with complex PLMFs, leading to superior performance in reducing computational complexity as well as simplifying formulation. A depth discussion about the approach is conducted in this paper, along with a numerical case study to demonstrate its potential benefits.
fuzzy nonlinear programming, piecewise linear membership functions, modeling
1 INTRODUCTION
Mathematical programming is acknowledged as a rigorous model based optimization methodology. However, it is always confronted with the impacts of subjective or objective uncertainty involved in real problems. Alternatively, fuzzy mathematical programming has received growing attention since Bellman and Zadeh [1], and Zimmermann [2] introduced fuzzy decision and fuzzy linear programming theories, respectively. Numerous relevant studies have widely circulated in the literatures [3-6].
Membership functions are usually employed to represent people’s subjective preferences or acceptances of objective uncertainty. Fuzzy mathematical programming can be converted into crisp one through constructing appropriate membership functions associated with fuzzy variables before achieving satisfactory optimal solutions. Practically, complex nonlinear membership functions are always used to accurately represent people’s thinking on the one but deepen nonlinearity and complexity of the problems on the other hand. In this regard, piecewise linear membership functions instead of nonlinear ones are highly advisable.
Piecewise linear functions(PLFs) were firstly introduced by Garvin et al. [7], which have been used in the areas of drilling, production, manufacturing, marketing and distribution. Subsequently, Henry [8] introduced construction methods of PLFs. After that, PLFs have been studied extensively, even being used to solve large-scale engineering problems in recent years [9-12]. Since the pioneer work of Narasimhan [13] and Hannan [14], problem with piecewise linear membership functions (PLMFs) have been introduced into the fuzzy programming and decision-making community. Taking advantage of appropriate assignment of sub-segments, PLMFs could approximate any nonlinear functions in expected fidelity. Thanks to the linearity of the segments, it is expected that the nonlinearity of a fuzzy nonlinear programming (FNLP) formulation could be somewhat indifferent to the membership functions. Traditionally, additive binary variables are usually demanded to formulate FNLP with piecewise linear membership functions. For instance, an efficient approach to formulating simple S-shape membership functions with binary variables was proposed by Yang et al [15]. Later, Li and Yu [16] showed that the method of Yang et al. would demand extra binary variables in the face of complex piecewise linear membership functions, thereby solved this problem by adding extra satisfaction degrees. Lin and Chen [17] suggested that the relations among the sub-segments could be expressed by intersections and unions, so that extending the method of Yang et al. to handle fuzzy programming problem with complex piecewise linear membership functions. Practically, three shortcomings of this kind method were identified, including (1) generalized procedure or algorithms unavailable; (2) requirement of extra binary variables sometimes; and (3) actual aspiration level unachievable. Besides, Chang [18] employed a couple of binary numbers to represent the relationship among binary variables, which became the first generalized algorithm concerning fuzzy programming with piecewise linear membership functions. However, in some cases the utilization of binary variables would lead to constraint-free problems. In response, Wen and Li [19] proposed a more comprehensive modeling methodology.
However, suffering the difficulty of binary variables assignments, the above-mentioned methodologies are no longer applicable in the face of complex PLMFs.
Motivated by these challenges, this study proposes a novel approach free of extra binary variables to formulate a FNLP problem, which could not only make the formulation simple but also reduce the computational complexity from NP-hard to polynomial-time problems [20, 21]. The rest of the paper is organized as follows. In Section 2, simple and complex cases ofPLMFs are extensively discussed. Besides, the problems encountered when solving the fuzzy programming with complex PLMFs are shown. Section 3 presents the approach to formulating FNLP with complex PLMFs. To demonstrate the usefulness of the proposed method, exemplary case studies are provided in Section 4. Finally, concluding remarks are given in Section 5.
2 PIECEWISE LINEAR MEMBERSHIP FUNCTIONS
2.1 Basic types
Basic PLMFs are composed of a number of linear segments, presenting S-shaped types usually, as shown in Fig. 1.
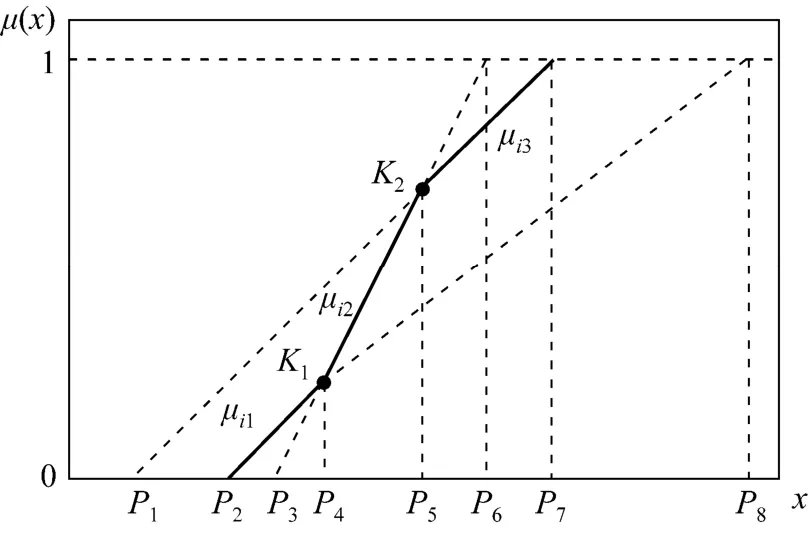
Figure 1 S-shaped membership function
In this example, three ramp-type membership functions μi1, μi2and μi3are involved, which are expressed as follows:

where K1and K2represent the convex and concave points, respectively. The integrations of two functions intersected with concave and convex points can be represented by intersection and union sets respectively. Accordingly, ()χμ can be specified asThe intersection set indicates “or” relation where each segment involved need not to be separated, while the union set indicates “parallel” relation where each segment involved should be distinguished.
As a key step for constructing PLMFs, traditional methods distinguish intersection with union by employing additive binary variables. For example, a fuzzy programming with membership functions shown in Fig. 1 can be addressed as follows.
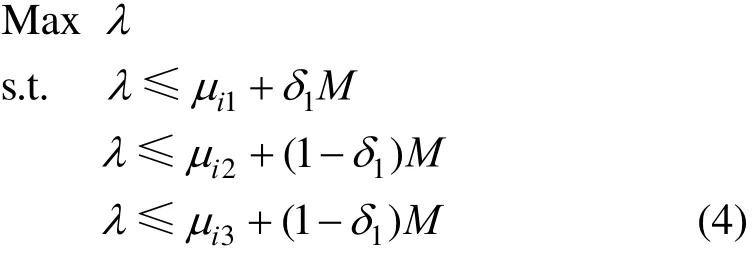
where M represents a big positive value, λ indicates the satisfaction degree, and δ1is an additional binary variable.
In the case of11δ=, the constraints becomeBecause M is a big positive number, the two latter constraints become inactive. While in the case of10δ=, the constraints arewhere the first one become inactive, leading toThus, it makes sense to consider that a feasible region can be completely described by means of transformation of binary variables.
2.2 Complex types
2.2.1 Introduction of compleχ form
Complex piecewise linear membership functions can be identified as a class of PLMFs with many convex and concave points, even with constant segments.
As a typical complex PLMF, the trapezoidal membership function presents a special bilateral form where the extreme is an interval rather than a point. This form of membership functions is in accordance with the practical issue which strongly demands interval representation. In practice, Gaussian functions always substitute both linear sides of typical trapezoidal membership functions, turning out to be nonlinear membership functions, as depicted in Fig. 2. Currently, it still remains an intractable problem to solve FNLP with nonlinear membership functions. Instead, this trapezoidal nonlinear membership function could be transformed into a trapezoidal PLMFs as shown inFig. 3, which contains 7 segments, 2 convex points (A1, A2), 4 concave points (B1, B2, B3, B4) and a constant function (μi4). Consequently, both sides of the function are constructed by a right and a left S-shape membership functions, respectively.
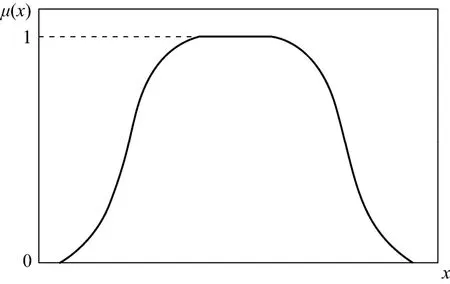
Figure 2 Trapezoidal nonlinear membership function
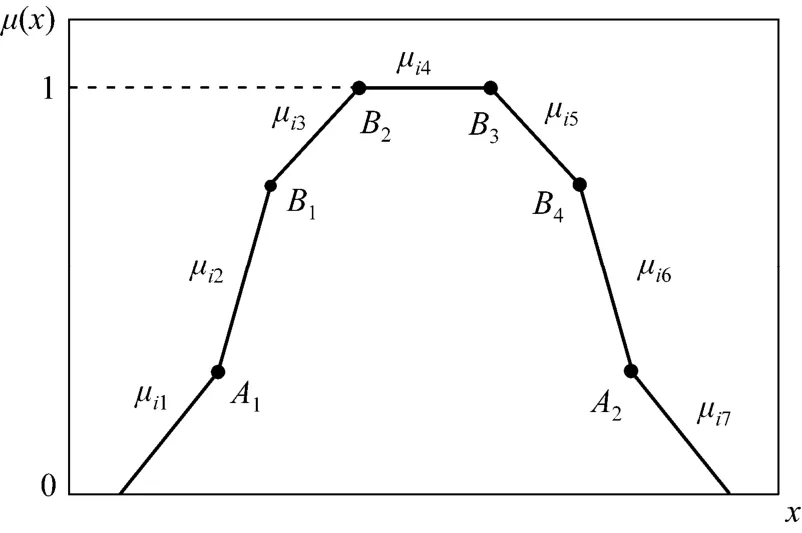
Figure 3 Trapezoidal PLMFs
2.2.2 Limitation of traditional methodology
It is convincible that traditional methods might fail to formulate FNLP with complex trapezoidal PLMFs. Taking the following two main types of error conditions for example.
Condition 1, the error may occur when one function is constrained by many constraints. PLMFs with 2 convex and 2 concave points and an additional function μ6are shown in Fig. 4. If a FNLP problem is constrained by the membership functions mentioned above, the optimal solution should be identified as the point C apparently.
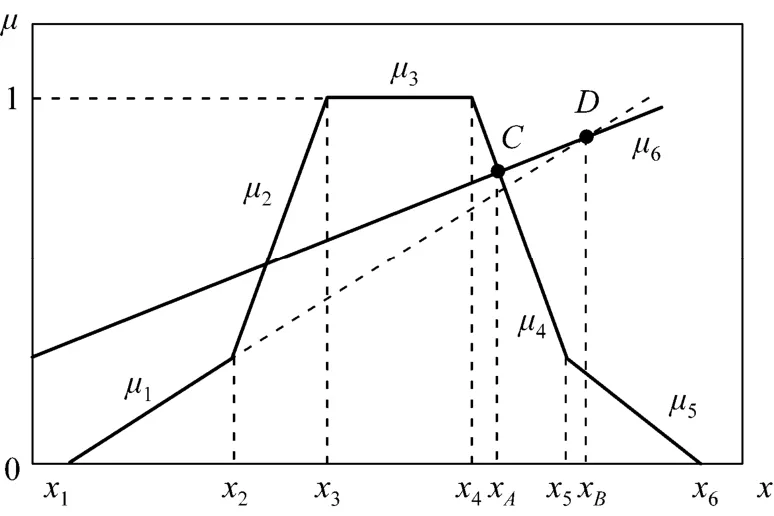
Figure 4 Modeling of trapezoidal PLMFs
However, the situation would be quite different if we formulate the problem with traditional methods as follows.
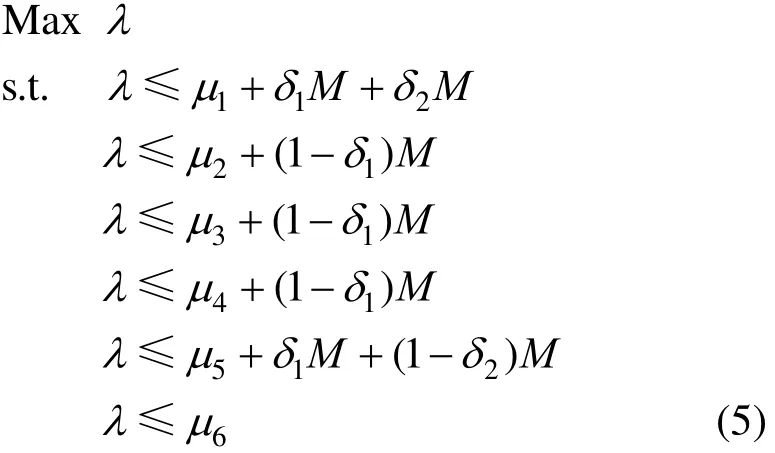
where, δ1and δ2are additional binary variables. In the presence of δ1=δ2=0, the latter four constraints become inactive because that M is a big positive number. Thus, the formulation can be simplified as:

It is apparent that λ is only confined by μ1and μ6which intersect mutually at point D. The satisfaction degree λ is constrained either by μ1when χ≤χBor by μ6when χ>χB. Because μ6is a monotonously increasing function, the restriction for λ is relaxing gradually with the χ which eventually leads to positive infinity of optimizing λ. Obviously, it is a wrong solution which implies that the traditional methods are unqualified to solve FNLP with complex PLMFs.
Condition 2, the error may also occur when the values of slopes of sub-segments are special. Taking the following fuzzy programming as an example.
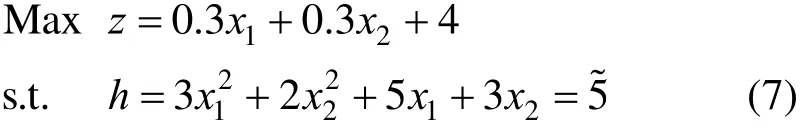
We initially obtained the optimum solutions of the corresponding crisp optimization problem as: χ1=0.213, χ2=0.819, z=4.31.
PLMFs without constant sub-segment for the constraints are constructed as shown in Fig. 5, where μ1and μ2, μ3and μ4are connected by convex points, and μ2and μ3are connected by concave point. The four segments can be expressed as: μ1=0.1608h+0.044, μ2=0.22h?0.1, μ3=?0.22h+2.1 and μ4=?0.1608h+ 1.652, respectively. By the floating of right-hand side, it is expected that the objective function z can reach 5, so the membership function of objective function can be expressed as: μz=(0.3χ1+0.3χ2+4)/5. Thus, the problem could be formulated by traditional methodology as follows.
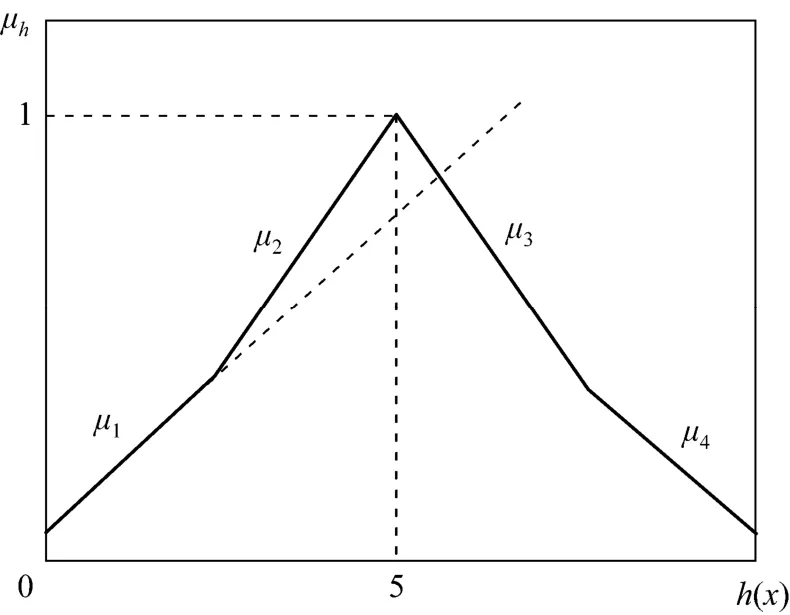
Figure 5 Complex PLMFs without constant segments
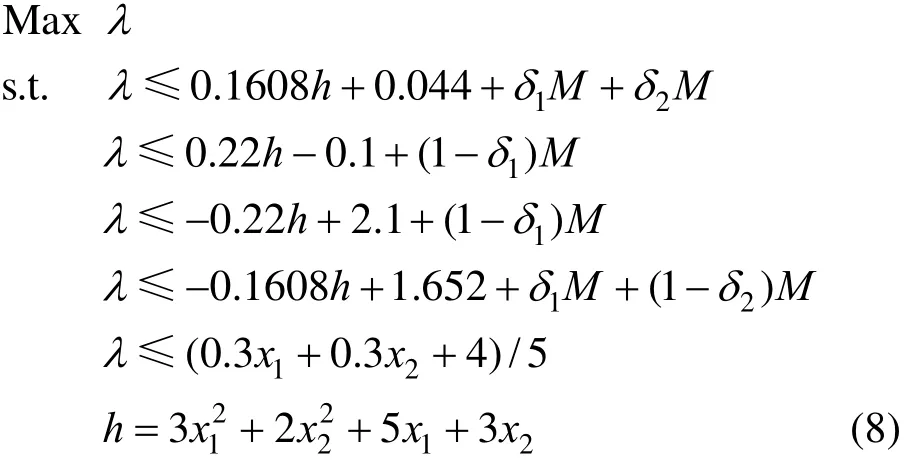
where,1δ and2δ are additional binary variables, and M is a big positive number. The optimal solutions of this model are achieved at11δ= and20δ=, as10.251 χ=,20.876 χ=, 4.34z=, 5.602 h= and 0.868 λ=.
In the situation of11δ=,20δ=, Eq. (8) can be simplified and re-arranged as follows.
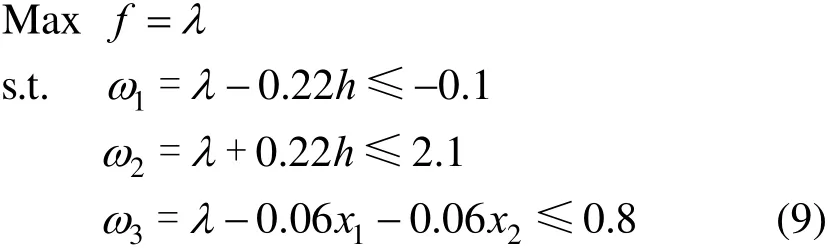
At the optimal solution, the active constraints must satisfy KKT conditions which are also known as the first order necessary conditions of optimality. Regarding Eq. (9), the KKT conditions are expressed by:
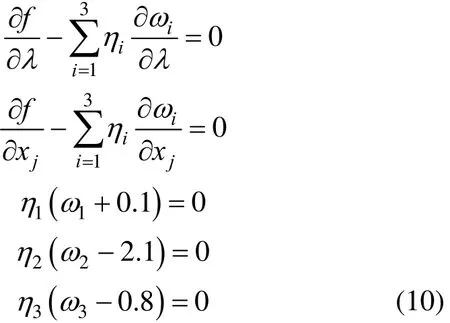
where1η,2η and3η are the vectors of KKT multipliers corresponding to each constraint. To perform algebraic calculations, the solutions of Eq. (10) could be obtained as10η=,20.036 η= and30.964 η=, which implies the optimality of the solutions.
But if solving the problem by general algebraic modeling system (GAMS), instead of this optimal solution, a very big one is obtained at10δ= and20δ=. Due to the satisfaction degree must less or equal to 1, this solution is wrong.
In the situation of10δ= and20δ=, Eq. (8) can be simplified and re-arranged as follows.1
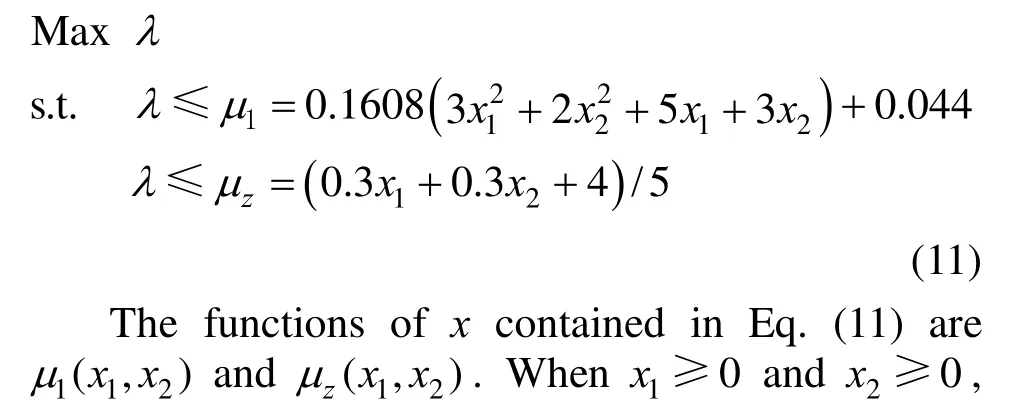
μ andzμ are the increasing functions of1χ and2χ. Now, the satisfaction degree λ is constrained only by zμ and1μ. Thus, when1χ and2χ increase, the constraint for λ will relax by the increasing ofzμ and1μ, which will make λ increase unlimitedly. As this is a maximum programming, the right solution achieved at 11 δ= and20δ= will be replaced by the unlimited one achieved at10δ= and20δ=, and cause solving error. Through the two examples mentioned above, the obvious drawback in traditional methodology caused by binary variables, has been proved.
3 A NOVEL APPROACH
It can be seen from the above example that in attempt to distinguish the different segments of PLMFs the utilization of binary variables may result in a severe fault. In response, a function which can distinguish the segments in different intervals is suggested to substitute binary variables, such as:
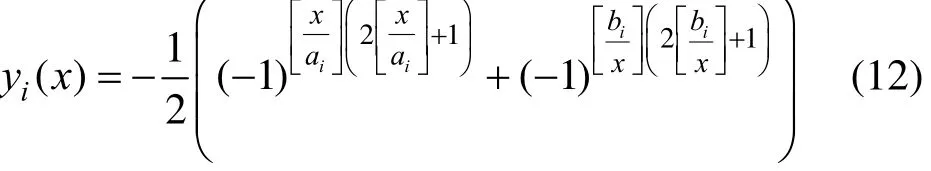
where [·] denotes the Gaussian rounding function, and aiand biare both sides abscissa of the ith segment subject toiiab<.
This function may reveal separate characteristics in different intervals, such as: (1) Wheniiabχ<<, because of
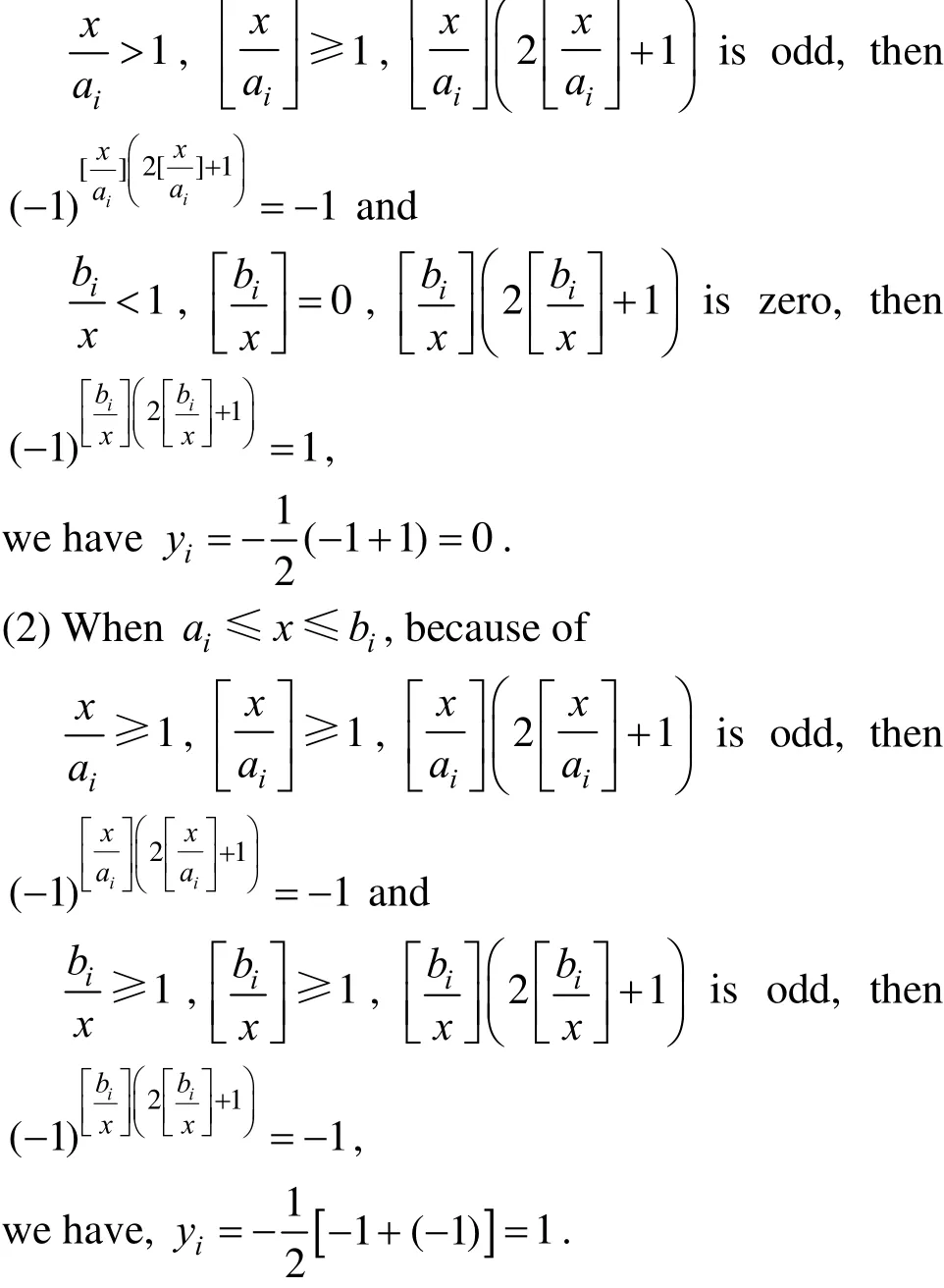
(3) Wheniiχab<<, because of
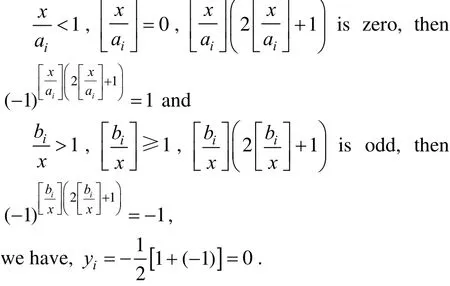
Apparently,iy equals to 1 only when χ belongs to interval (,)iiab, otherwise it equals to 0. The segments could be appropriately switched by means of this function, which results in a holistic expression of the PLMFs.
With this approach, a fuzzy programming problem with complex linear membership functions can be formulated as follows.
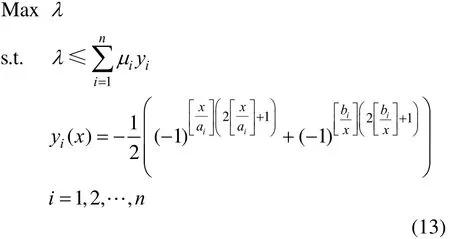
where λ represents the satisfaction degree,iμ is the function of the ith segment, andia andib are both sides abscissa of the ith segment withiiab<. Thus, the segments could be switched with the abscissa changing, leading to a reasonable expression of the satisfaction subject to constraints free of binary variables.
4 ILLUSTRATIVE EXAMPLES
The feasibility and simplicity of the proposed methodology is further proved by the following two examples, respectively.
(1) A numerical example
Considering the membership functions shown in Fig. 4, where11χ=,23χ=,34χ=,46χ=,57χ= and69χ=, the fuzzy programming formulations by proposed approach are presented as follows.
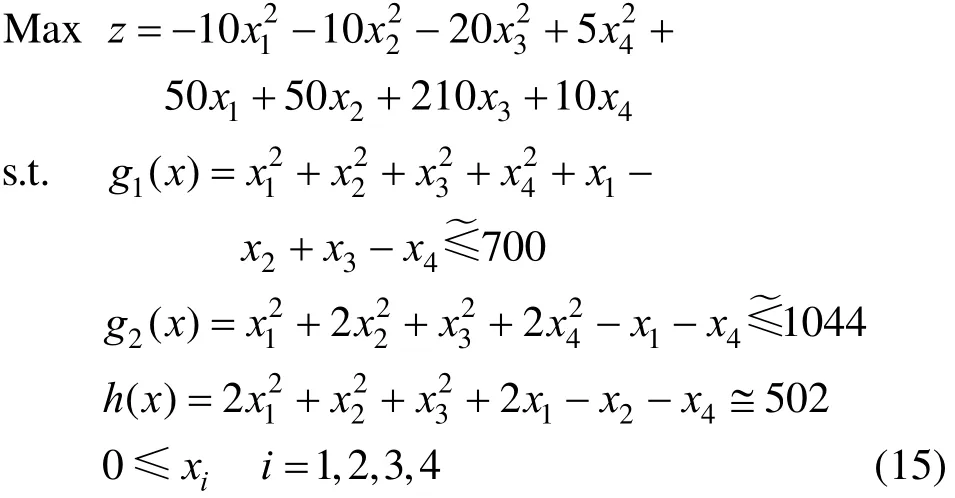
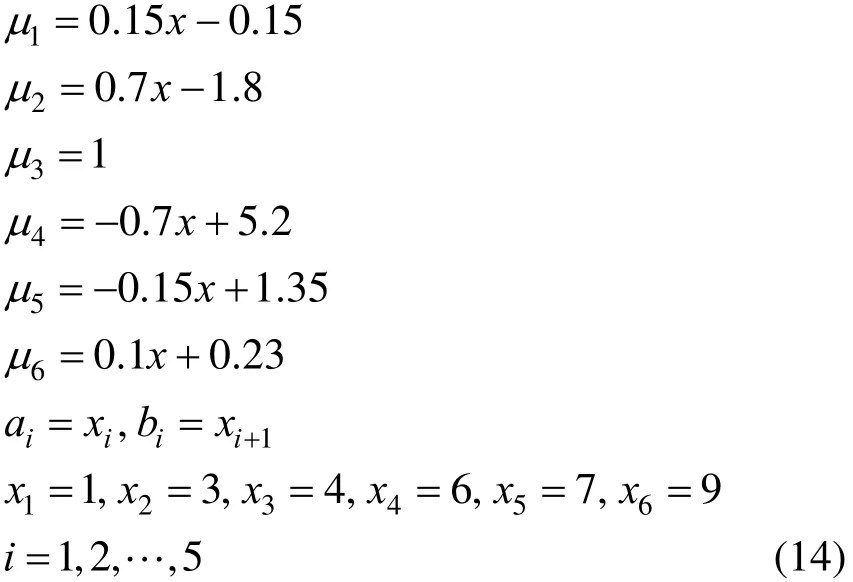
This nonlinear programming problem was solved by CONOPT solver of GAMS, resulting in optimum solutions as 6.21χ?= and 0.851 λ?= which are obviously reasonable because the point (6.21, 0.851) is accordance with the position of point C, as shown in Fig. 4. It is clear that the benefit of this approach lies in the solutions far from the faults caused by additive binary variables and the constraints less used than those of traditional methods.
(2) An application example
Consider workshop production planning problems in an oil refinery. Achievement of the best economic benefits are usually constrained by many demands, such as: limited resources, reasonable product specifications, processing strategies, lower energy consumptions and so on. Therefore, establishments of an appropriate mathematical model which can reflect the relationship between comprehensive factors is crucial to workshop production planning.
The following fuzzy nonlinear programming problems are formulated from a realistic workshop production planning background.
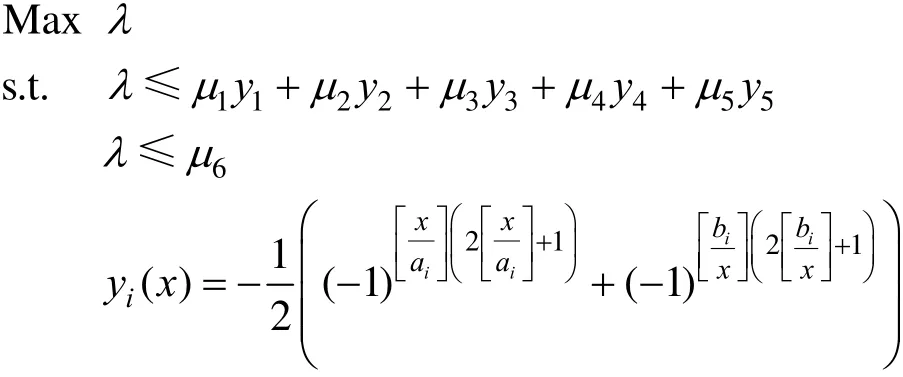
where,14~χχ are the yield of the 4 production, respectively. The solutions of the crisp model are:115χ=,23χ=,36χ=,420χ=, 1300z=.
In the realistic situations, a delayed production schedule always leads to difficulties to achieve the target profits. In response, we have to specify some reasonable relaxations to the constraints, which consequently turns the planning problem into a fuzzy programming formulation. For instance, we may change the constraints in model 15 into fuzzy one, which means that the constraints can be exceeded in a reasonable range. Here we use PLMFs to describe the corresponding fuzziness, which are:

To specify 1500 as the goal of profits, by the proposed modeling methodology, the fuzzy formulation of model 15 can be change into follows.

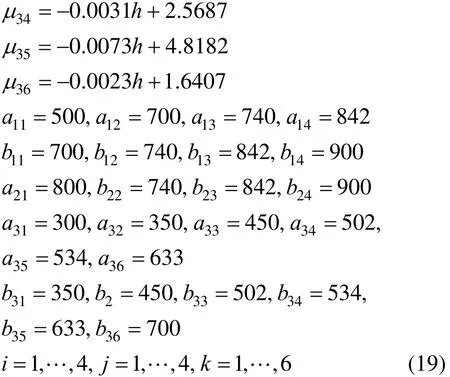
The results obtained with the CONOPT solver of GAMS are114.809χ?=,22.25χ?=,36.049 χ?=,420.352χ?=, 0.948λ?=, 1422.349 z?=, which shows that the profit is increased significantly with the reasonable relaxation of constraints, eventually completing the schedule in time.
In contrast, the model 19 was also dealt with by the methodology presented in [22] with the same solver of GAMS. The results of both methodologies are listed in Table 1, which show that the proposed approach is superior to the traditional one in terms of time consumption.

Table 1 Result comparison
5 CONCLUSIONS
After pointing out the defects of traditional methodologies applied to the formulation of fuzzy nonlinear programming with complex PLMFs, a novel approach was explicitly presented in this paper. By means of constructing a new function, the assignable causes of methodological failure associated with traditional approaches were definitely eliminated along with a simple formulation. Compared with the traditional methodologies, this approach has been proved to be more efficient because of less resource usage and iteration time consuming.
NOMENCLATURE
AiConvex point
aiLeft-hand side abscissa of segment
BiConcave point
biRight-hand side abscissa of segment
M Big positive number
δiBinary variable
ηiKKT multiplier
λ Satisfaction degree
μijSub-segment of PLMFs
REFERENCES
1 Bellman, R.E., Zadeh, L.A., “Decision-making in a fuzzy envrionment”, Management Science, 17, 141-164 (1970).
2 Zimmermann, H.J., “Fuzzy programming and linear programming with several objective functions”, Fuzzy Sets and Systems, 1, 45-55 (1978).
3 Zimmermann, H.J., Fuzzy Sets, Decision Making and Expert Systems, Kluwer, Boston (1987).
4 Roubens, M., Teghen, J., “Comparison of methodologies for fuzzy and stochastic multi-objective programming “, Fuzzy Sets and Systems, 42, 119-132 (1991).
5 Shi, T., Yu, P.L., “Selecting optimal production system in multiple criteria environments”, Computer & Operations Research, 19, 585-608 (1992).
6 Liu, Y.H., Shi, Y., “A fuzzy programming approach for solving a multiple criteria and multiple constraint level linear programming problem”, Fuzzy Sets and Systems, 65, 117-124 (1994).
7 Garvin, W.W., Crandall, H.W., John, J.B., Spellman, R.A., “Applications of linear programming in the oil industry”, Management Science, 3, 407-427 (1957).
8 Stone, H., “Approximation of curves by line segments”, Computer and Information Science, 15, 40-47 (1961).
9 Effati, S., Abbasiyan, H., “Solving fuzzy linear programming problems with piecewise linear membership functions”, Applications and Applied Mathematics: An International Journal, 5, 504-533 (2010).
10 Toriello, A., Vielma, J.P., “Fitting piecewise linear continuous functions”, European Journal of Operational Research, 219, 86-95 (2012).
11 Guo, W.S., Huang, H., Lü, Y., Li, G.C., “Waste management under multiple complexities: Inexact piecewise-linearization-based fuzzy flexible programming”, Waste Management, 32, 1244-1257 (2012).
12 Wen, C.T., Ma, X.Y., “A max-piecewise-linear neural network for function approximation”, Neurocomputing, 71, 843-852 (2008).
13 Narasimhan, R., “Goal programming in a fuzzy environment”, Decision science, 11, 325-336 (1980).
14 Hannan, E.L., “Linear programming with multiple fuzzy goals”, Fuzzy Sets and Systems, 6, 235-248 (1981).
15 Yang, T., Ignizio, J.P., Kim, H.J., “Fuzzy programming with nonlinear membership functions: Piecewise linear approximation”, Fuzzy Sets and Systems, 41, 39-53 (1991).
16 Li, H.L., Yu, C.S., “Comments on “Fuzzy programming with nonlinear membership functions...””, Fuzzy Sets and Systems, 101, 109-113 (1999).
17 Lin, C.C., Chen, A.P., “Generalization of Yang et al.’s method for fuzzy programming with piecewise linear membership functions”, Fuzzy Sets and Systems, 132, 347-352 (2002).
18 Chang, C.T., “Binary behavior of fuzzy programming with piecewise linear membership functions”, IEEE Transactions on Fuzzy Systems, 15, 342-349 (2007).
19 Wen, B., Li, H.G., “Modeling methodology for fuzzy programming with piecewise linear membership functions”, CIESC Journal, 61 (8), 2149-2153 (2010). (in Chinese)
20 Keha, A.B., de Farias, I.R., Nemhauser, G.L., “A branch-and-cut algorithm without binar variables for nonconvex piecewise linear optimization”, Operations Research, 54 (5), 847-858 (2006).
21 Agrali, S., Geunes, J., “Solving knapsack problem with S-curve return functions”, European Journal of Operational Research, 193, 605-615 (2009).
22 Wen, B., Li, H.G., “Approaches to building piecewise linear membership functions in nonlinear fuzzy programming”, CIESC Journal, 62 (8), 2258-2264 (2011). (in Chinese)
2012-10-23, accepted 2013-01-24.
*To whom correspondence should be addressed. E-mail: lihg@mail.buct.edu.cn
 Chinese Journal of Chemical Engineering2014年4期
Chinese Journal of Chemical Engineering2014年4期
- Chinese Journal of Chemical Engineering的其它文章
- One Step Preparation of Sulfonated Solid Catalyst and Its Effect in Esterification Reaction*
- Effects of Assistant Solvents and Mixing Intensity on the Bromination Process of Butyl Rubber*
- Determination and Correlation of Solubility for D-Xylose in Volatile Fatty Acid Solvents*
- Impacts of Power Density on Heavy Metal Release During Ultrasonic Sludge Treatment Process*
- Support Effects on Thiophene Hydrodesulfurization over Co-Mo-Ni/Al2O3and Co-Mo-Ni/TiO2-Al2O3Catalysts*
- Determination and Correlation of Solubilities of Four Novel Benzothiazolium Ionic Liquids with6PF?in Six Alcohols*
