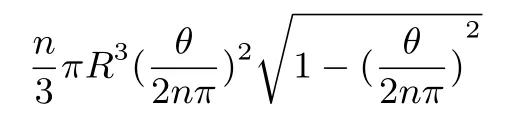由扇形制成多個圓錐的體積之和
——Jensen不等式的一個幾何應用
深圳市龍華區教育科學研究院附屬外國語學校(518109) 鐘文體
取一個圓,剪出兩個扇形,再圍成兩個圓錐.如何剪能使兩個圓錐的體積之和最大? 文[1]提出并解決了這個問題,其解答涉及一個三次方程的求解.文[1]的末尾還提出了這樣一個問題:對一般的扇形,如何分成兩個或多個扇形,使圍成的兩個或多個圓錐的體積之和最大? 本文使用Jensen 不等式部分地解決這個問題.
首先回顧凸函數的概念.
設f(x)是定義在區間I上的函數,若對任意x1,x2∈I及任意λ ∈(0,1),有f(λx1+(1?λ)x2) ≤λf(x1)+(1?λ)f(x2),則稱f(x)為I上的凸函數.若等號成立當且僅當x1=x2,則稱為嚴格凸函數.
關于凸函數,有著名的Jensen 不等式.
Jensen 不等式設f(x) 是I上的凸函數,若xi ∈ I,qi >0(i= 1,2,··· ,n) 且= 1,則f(q1x1+q2x2+···+qnxn)≤q1f(x1)+q2f(x2)+···+qnf(xn).若f(x) 為嚴格凸函數,則等號成立當且僅當x1=x2=···=xn.下面的引理可以很方便地判斷給定函數是否為凸函數.
引理設f(x)在區間I上有二階導數,且對?x ∈I,有f′′(x) ≤0,則f(x)是I上的凸函數.若不等號嚴格成立,則為嚴格凸函數.有了這些準備,我們可以證明下述結論.
命題設扇形的半徑為R,圓心角θ≤187.5°.將這個扇形分成n個小扇形,再圍成n個圓錐.則當這n個小扇形的圓心角相等時,所圍成n個圓錐的體積之和取最小值當這n個小扇形中有一個的圓心角趨于θ,其余的圓心角趨于0 時,所圍成n個圓錐的體積之和趨于.且不管怎么分,所圍成的圓錐體積之和都不超過
證明設小扇形的圓心角分別為αi(i= 1,2,··· ,n),所圍成的圓錐的底面半徑為ri,則α1+α2+···+αn=θ,Rαi= 2πri.故ri=圓錐的母線長都為R,故高分別為hi=于是,圓錐的體積之和為
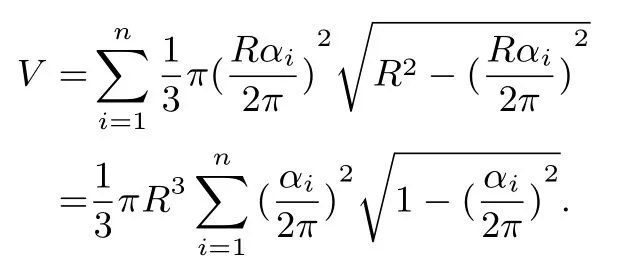
考慮函數f(x) =ai,則V=簡單的計算得f′(x) =從而f′(x)>0?x ∈ f′′(x)>0?x ∈于是f(x)在上嚴格遞增,在上嚴格凸.
由條件可知ai∈故由Jensen 不等式,有等號成立當且僅當a1=a2=···=an,即當且僅當α1=α2=···=αn.從而
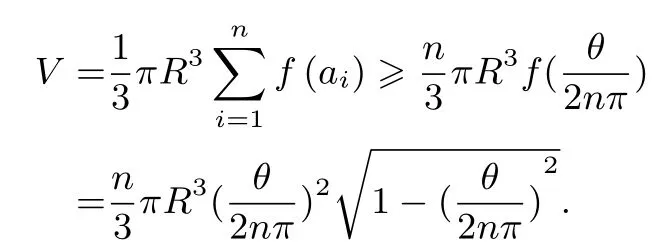
另一方面,設xi且x1+x2+···+xn≤我們證明f(x1)+f(x2)+···+f(xn) ≤f(x1+x2+···+xn),且等號成立當且僅當x1,x2,··· ,xn中有n ?1 個為零.用數學歸納法.設n= 2.當x1,x2中有一個為零時,結論顯然成立.不妨設0?=x1≤x2.考慮函數g(x) =f(x1+x)?f(x),x ∈
求導得g′(x) =f′(x1+x)?f′(x).因x,x1+x ∈由前面的論述可知f′(x) 在上嚴格遞增,故g′(x) =f′(x1+x)?f′(x)>0.
于是,g(x)在上嚴格遞增.從而g(x) ≤g(0),即f(x1+x) ≤f(x1)+f(x),且等號成立當且僅當x= 0.特別地,f(x1+x2)> f(x1)+f(x2).故n= 2時,結論成立.
假設n=k時,結論成立,即f(x1) +f(x2) +···+f(xk)≤f(x1+x2+···+xk).那么,n=k+1 時,
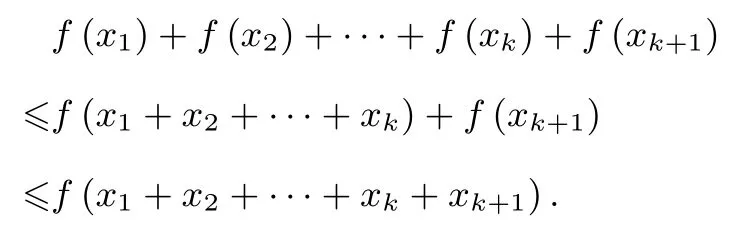
根據歸納假設,第一個等號成立的條件為x1,x2,··· ,xk中有k?1 個為零;第二個等號成立的條件為x1+x2+···+xk和xk+1中有一個為零.由此不難得到上述不等式中等號成立的條件為x1,x2,··· ,xk+1中有k個為零.從而結論成立.特別地,有
注1圓心角θ >時如何處理是個值得思考的問題,留給讀者作進一步的思考.
注2可以證明n增大時,最小值