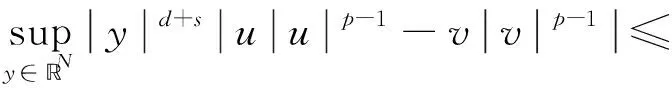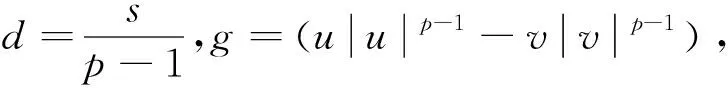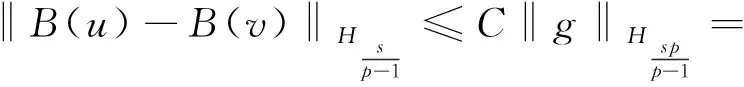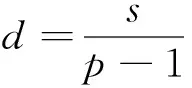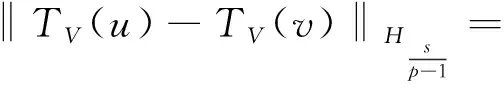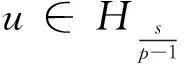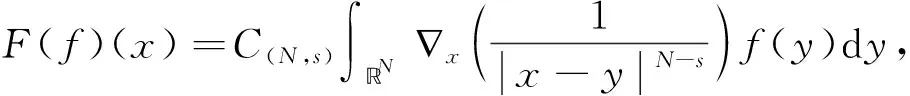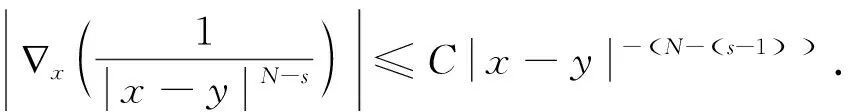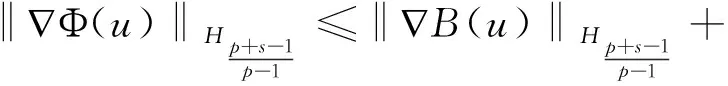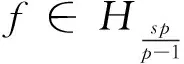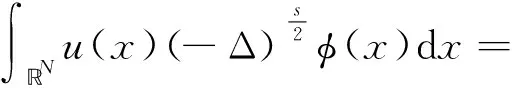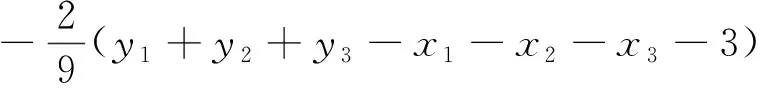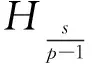具分數階Laplace算子的非線性橢圓方程解的存在性
林巧兒, 原子霞
(電子科技大學 數學科學學院, 四川 成都 611731)
0 引言
本文研究具分數階Laplace算子的非線性橢圓方程
(1)
當函數V(x)和f(x)均為0并且s=2時,方程(1)就變成了著名的Lane-Emden方程
-Δu=u|u|p-1,
(2)
后來,學者們開始研究在方程(2)右端加上一個線性項V(x)u的方程
-Δu=u|u|p-1+V(x)u.
(3)
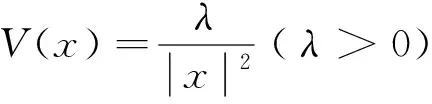
除此之外,學者們也研究了在方程(2)右端加上一個非線性項f(x)的Lane-Emden方程,即
-Δu=u|u|p-1+f(x).
(4)
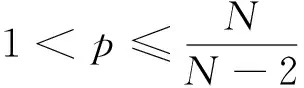
分析上述文獻,不難看出線性項V(x)u和非線性項f(x)對方程(2)的解的存在性具有一定的影響,并且這些方程被廣泛應用于物理領域中,可見研究在方程(2)右端添加了線性項V(x)u和非線性項f(x)解的存在性問題具有一定的理論和實際意義. 此外,由于具分數階Laplace算子的偏微分方程比具整數階Laplace算子的偏微分方程解釋實際問題更為準確.因此,本文將在N空間上研究方程(1)的解的存在性.
實際上,當函數V(x)和f(x)均為0時,方程(1)就變為了
(-Δ)su=u|u|p-1,x∈N.
(5)
下面我們討論當函數V(x)≥0,f(x)>0時,方程(1)解的存在性.為了方便后續證明,我們考慮方程(1)的積分等價方程
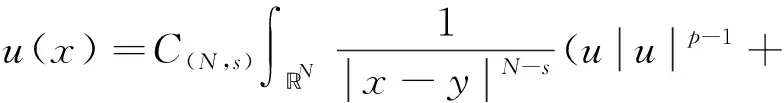
(6)
首先,我們將上式右端分解為以下三項
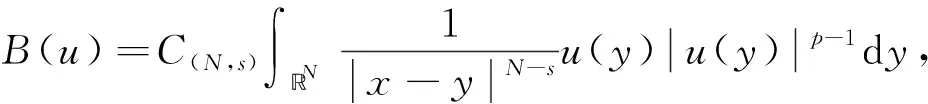
現在假設u(x)是方程(1)的一個解,我們定義伸縮變換
(7)
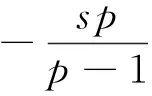
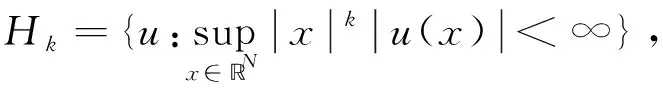
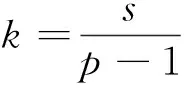
本文的主要結構安排如下:第1節解釋文中出現的一些符號;第2節介紹一些定義以及本文的主要定理;第3節給出后續證明所需的幾個重要引理;第4節證明方程(1)解的存在唯一性,并且證明了它是分布意義下的弱解. 進一步地,我們還證明了解與函數V(x)和f(x)相關的性質.
下文,我們用C表示與R,x無關的常數,它可以逐行變化.
1 符號與注釋
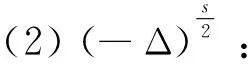
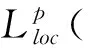
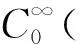
(5)C(N,s):與N和s有關的常數.
(6)Δ:Laplace算子.
(7)?:梯度.
(8)Hk:Banach空間
(9)‖·‖Hk:Hk空間中的范數.
2 主要定理
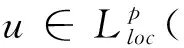
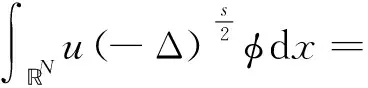
則稱u是方程(1)在N上的弱解.
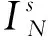
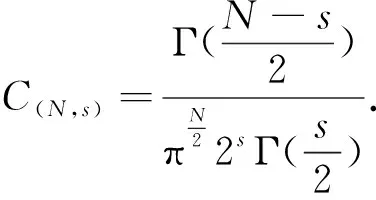
因此,通過計算可知方程(1)的積分等價方程為
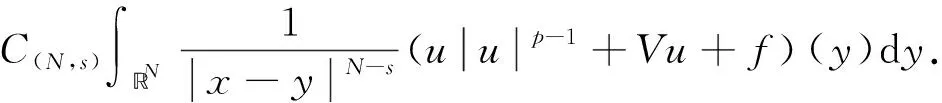
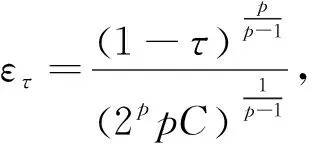
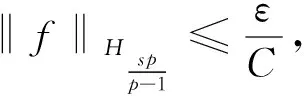
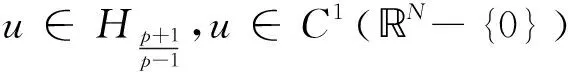
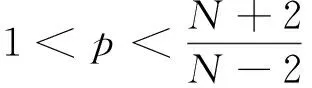
(3)特別地,當
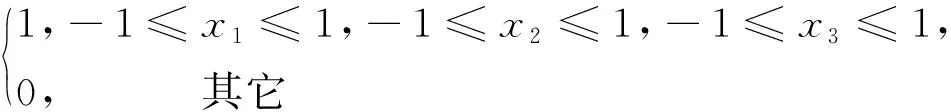
時,方程(1)在(0,0,0)點處數值解的近似值為1.2870e+194.
定理2(1)若函數V(x)≥0,f(x)>0(或V(x)≥0,f(x)<0)對x∈N一致成立,則解u(x)是正的(或u(x)是負的).
(2)若函數f(x)是徑向的(或f(x)不是徑向的),V(x)是徑向的,則解u(x)是徑向的(或u(x)不是徑向的).
(3)在(1)成立的前提條件下,若函數f(x)是徑向的但V(x)不是徑向的,則解u(x)不是徑向的.
3 主要引理
本節介紹并證明一些引理,這些引理對于后面證明主要定理至關重要.
引理1[17]設0<α 引理3設X是一個范數為‖·‖X的Banach空間,T:X→X是一個連續線性映射,‖T‖≤τ<1,ρ>0,B:X→X是一個映射且滿足B(0)=0和 (8) 證明定義映射Φ:X→X,且Φ(x)=y+T(x)+B(x).若 則有 這就證明了Φ(Aε)?Aε.此外,?x,z∈Aε,有 引理4設0 ‖F(g)‖Hd≤C‖g‖Hd+s (9) 成立. 此外,若g∈Hd+s,則?F(g)∈Hd+s-1且F(g)∈C1(N-{0}). 證明利用算子F的定義,在引理1中取α=N-(d+s),β=s,則有 (10) 其中 再利用引理1就可以得到 (11) 其中對于每一個固定的x都有 我們利用引理1可得 定理1的證明:(1)利用Mazur不等式可得 (12) (13) (14) 并且有 因此,u是分布意義下的弱解. 定理1得證. (3)由于方程(1)存在唯一解,該解可以看作是下列Picard序列的極限: u1=F(f), um+1=F(f)+B(um)+TV(um),m∈N. 不妨考慮N=3的情況. 在方程(1)中取s=1,q=2,V(x)=0, 定理2的證明:(1)我們可以將解u看作是下列Picard序列的極限: u1=F(f), um+1=F(f)+B(um)+TV(um),m∈N. 由算子F的定義可知,當函數f(x)>0對x∈N一致成立時,有F(f)>0,于是u1=F(f)>0.設um>0,由數學歸納法可知,只要函數V(x)≥0對于x∈N一致成立,就有um+1=F(f)+B(um)+TV(um)>0.由于解u是序列{um}的極限,即又因為F(f)>0,于是u=F(f)+B(u)+TV(u)>0.同理可證解u為負的情況. (3)不妨假設函數V(x)≥0,f(x)>0對x∈N一致成立,即u>0.假設u是徑向的,由于f(x)是徑向的,所以TV(u)=u-F(f)-B(u)是徑向的,根據算子TV的定義可知Vu是徑向函數. 由于u>0且是徑向的,于是函數V(x)是徑向的,這與假設V(x)不是徑向的矛盾,所以解u不是徑向的. 定理2得證.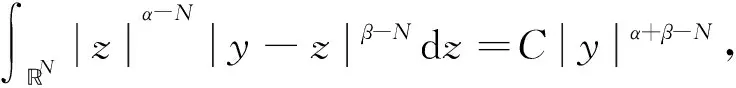
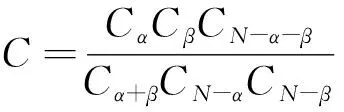
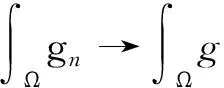
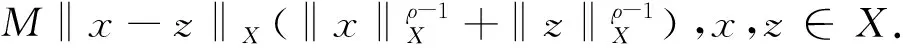
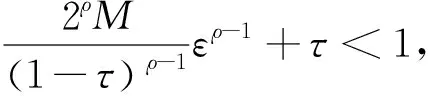
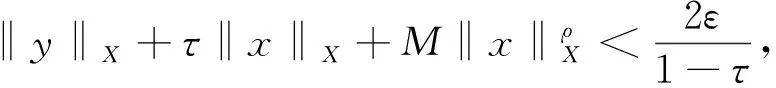
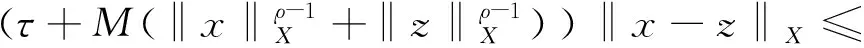
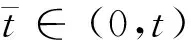
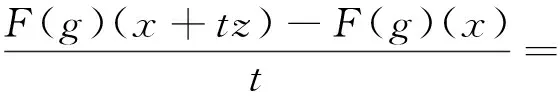
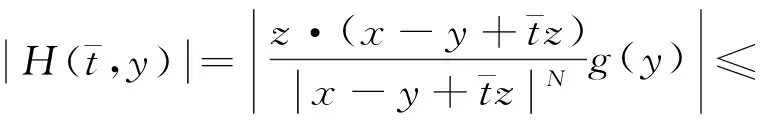
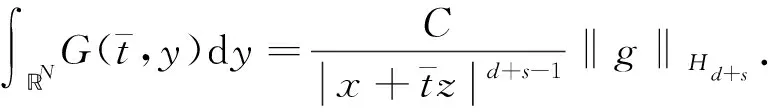
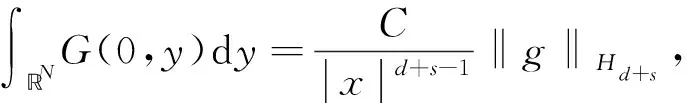
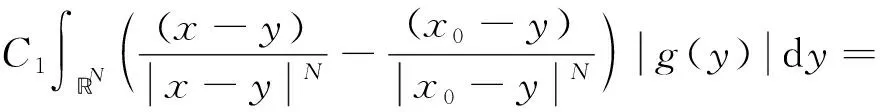
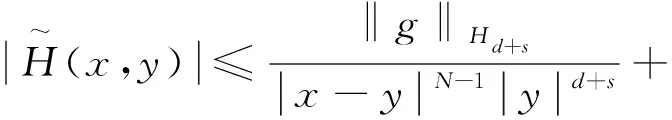
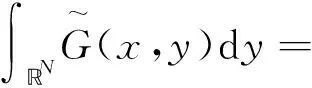
4 主要結果